Paul Viallard
LHC
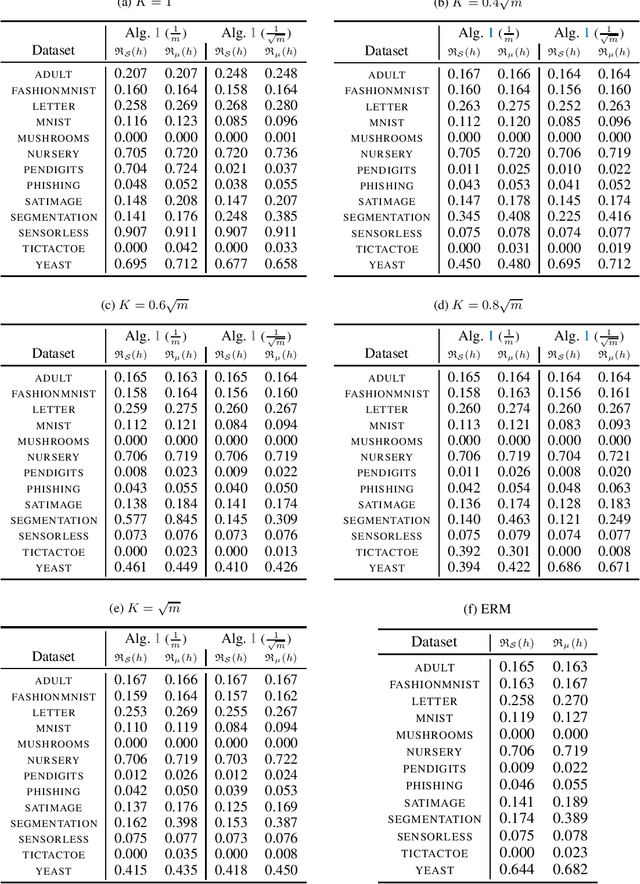
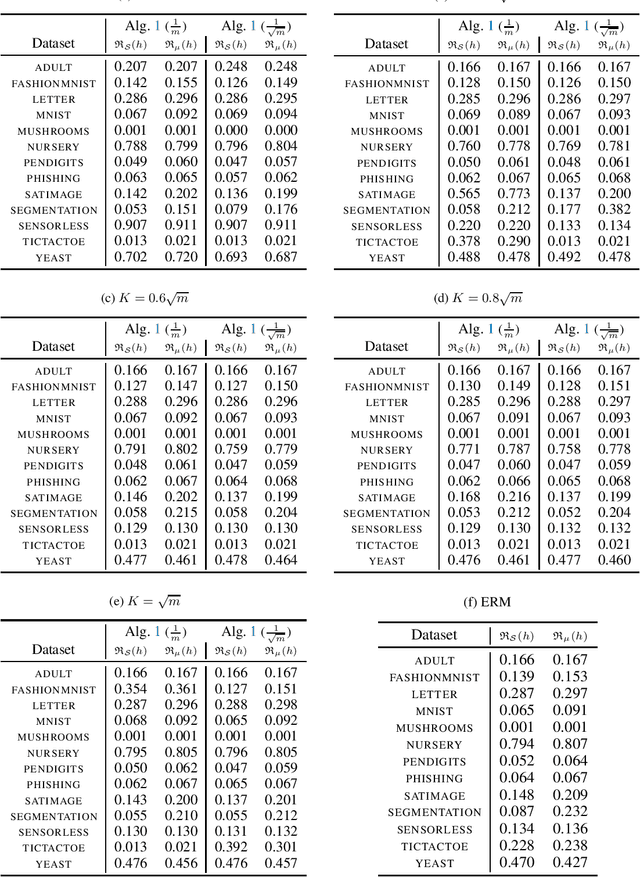
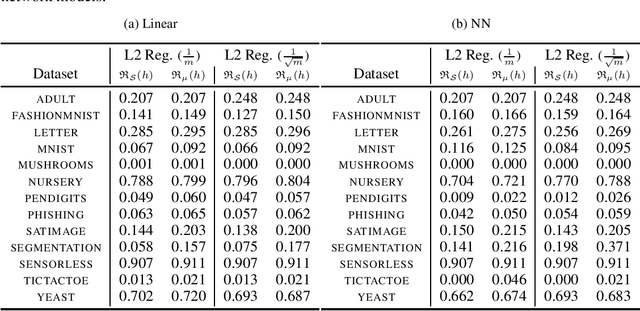
Uniform Generalization Bounds on Data-Dependent Hypothesis Sets via PAC-Bayesian Theory on Random Sets
Apr 26, 2024Abstract:We propose data-dependent uniform generalization bounds by approaching the problem from a PAC-Bayesian perspective. We first apply the PAC-Bayesian framework on `random sets' in a rigorous way, where the training algorithm is assumed to output a data-dependent hypothesis set after observing the training data. This approach allows us to prove data-dependent bounds, which can be applicable in numerous contexts. To highlight the power of our approach, we consider two main applications. First, we propose a PAC-Bayesian formulation of the recently developed fractal-dimension-based generalization bounds. The derived results are shown to be tighter and they unify the existing results around one simple proof technique. Second, we prove uniform bounds over the trajectories of continuous Langevin dynamics and stochastic gradient Langevin dynamics. These results provide novel information about the generalization properties of noisy algorithms.
Leveraging PAC-Bayes Theory and Gibbs Distributions for Generalization Bounds with Complexity Measures
Feb 19, 2024
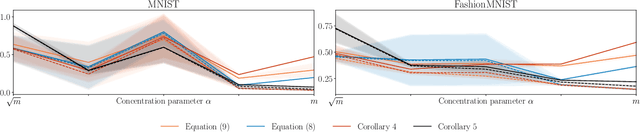
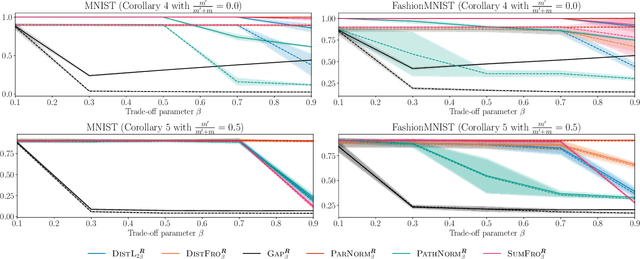
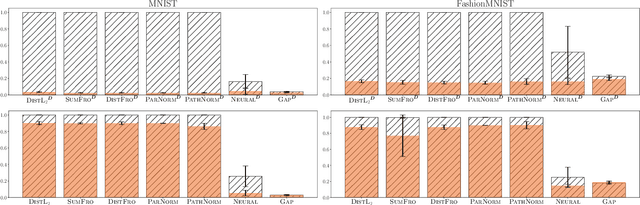
Abstract:In statistical learning theory, a generalization bound usually involves a complexity measure imposed by the considered theoretical framework. This limits the scope of such bounds, as other forms of capacity measures or regularizations are used in algorithms. In this paper, we leverage the framework of disintegrated PAC-Bayes bounds to derive a general generalization bound instantiable with arbitrary complexity measures. One trick to prove such a result involves considering a commonly used family of distributions: the Gibbs distributions. Our bound stands in probability jointly over the hypothesis and the learning sample, which allows the complexity to be adapted to the generalization gap as it can be customized to fit both the hypothesis class and the task.
A PAC-Bayesian Link Between Generalisation and Flat Minima
Feb 13, 2024
Abstract:Modern machine learning usually involves predictors in the overparametrised setting (number of trained parameters greater than dataset size), and their training yield not only good performances on training data, but also good generalisation capacity. This phenomenon challenges many theoretical results, and remains an open problem. To reach a better understanding, we provide novel generalisation bounds involving gradient terms. To do so, we combine the PAC-Bayes toolbox with Poincar\'e and Log-Sobolev inequalities, avoiding an explicit dependency on dimension of the predictor space. Our results highlight the positive influence of \emph{flat minima} (being minima with a neighbourhood nearly minimising the learning problem as well) on generalisation performances, involving directly the benefits of the optimisation phase.
Tighter Generalisation Bounds via Interpolation
Feb 07, 2024



Abstract:This paper contains a recipe for deriving new PAC-Bayes generalisation bounds based on the $(f, \Gamma)$-divergence, and, in addition, presents PAC-Bayes generalisation bounds where we interpolate between a series of probability divergences (including but not limited to KL, Wasserstein, and total variation), making the best out of many worlds depending on the posterior distributions properties. We explore the tightness of these bounds and connect them to earlier results from statistical learning, which are specific cases. We also instantiate our bounds as training objectives, yielding non-trivial guarantees and practical performances.
From Mutual Information to Expected Dynamics: New Generalization Bounds for Heavy-Tailed SGD
Dec 01, 2023Abstract:Understanding the generalization abilities of modern machine learning algorithms has been a major research topic over the past decades. In recent years, the learning dynamics of Stochastic Gradient Descent (SGD) have been related to heavy-tailed dynamics. This has been successfully applied to generalization theory by exploiting the fractal properties of those dynamics. However, the derived bounds depend on mutual information (decoupling) terms that are beyond the reach of computability. In this work, we prove generalization bounds over the trajectory of a class of heavy-tailed dynamics, without those mutual information terms. Instead, we introduce a geometric decoupling term by comparing the learning dynamics (depending on the empirical risk) with an expected one (depending on the population risk). We further upper-bound this geometric term, by using techniques from the heavy-tailed and the fractal literature, making it fully computable. Moreover, as an attempt to tighten the bounds, we propose a PAC-Bayesian setting based on perturbed dynamics, in which the same geometric term plays a crucial role and can still be bounded using the techniques described above.
Learning via Wasserstein-Based High Probability Generalisation Bounds
Jun 07, 2023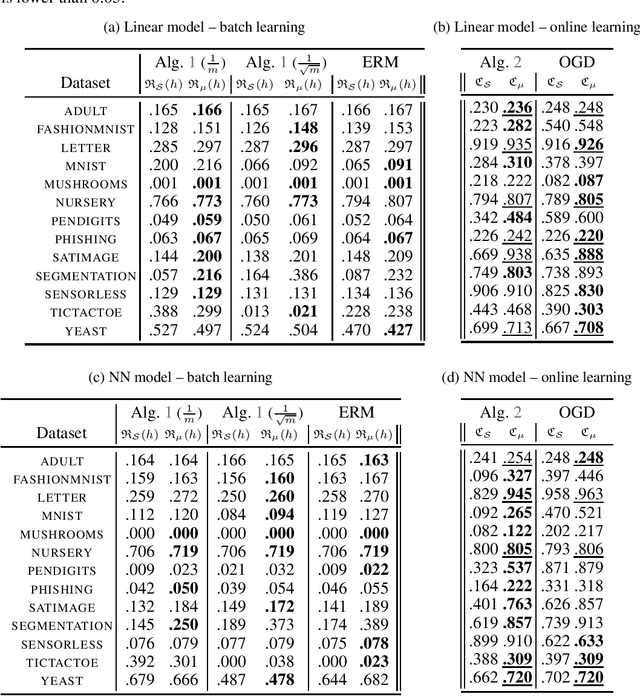
Abstract:Minimising upper bounds on the population risk or the generalisation gap has been widely used in structural risk minimisation (SRM) - this is in particular at the core of PAC-Bayesian learning. Despite its successes and unfailing surge of interest in recent years, a limitation of the PAC-Bayesian framework is that most bounds involve a Kullback-Leibler (KL) divergence term (or its variations), which might exhibit erratic behavior and fail to capture the underlying geometric structure of the learning problem - hence restricting its use in practical applications. As a remedy, recent studies have attempted to replace the KL divergence in the PAC-Bayesian bounds with the Wasserstein distance. Even though these bounds alleviated the aforementioned issues to a certain extent, they either hold in expectation, are for bounded losses, or are nontrivial to minimize in an SRM framework. In this work, we contribute to this line of research and prove novel Wasserstein distance-based PAC-Bayesian generalisation bounds for both batch learning with independent and identically distributed (i.i.d.) data, and online learning with potentially non-i.i.d. data. Contrary to previous art, our bounds are stronger in the sense that (i) they hold with high probability, (ii) they apply to unbounded (potentially heavy-tailed) losses, and (iii) they lead to optimizable training objectives that can be used in SRM. As a result we derive novel Wasserstein-based PAC-Bayesian learning algorithms and we illustrate their empirical advantage on a variety of experiments.
Learning Stochastic Majority Votes by Minimizing a PAC-Bayes Generalization Bound
Jun 23, 2021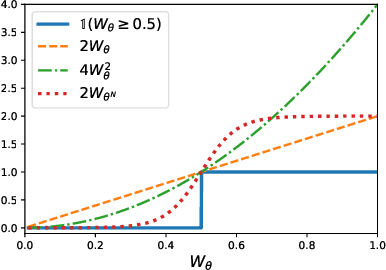
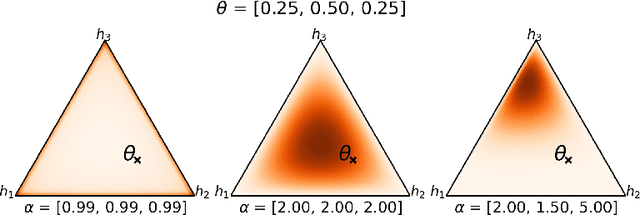
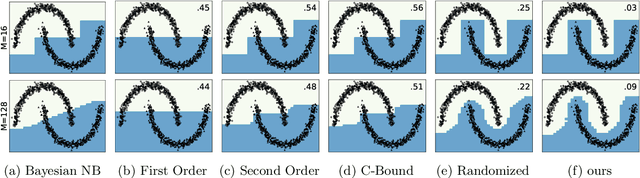
Abstract:We investigate a stochastic counterpart of majority votes over finite ensembles of classifiers, and study its generalization properties. While our approach holds for arbitrary distributions, we instantiate it with Dirichlet distributions: this allows for a closed-form and differentiable expression for the expected risk, which then turns the generalization bound into a tractable training objective. The resulting stochastic majority vote learning algorithm achieves state-of-the-art accuracy and benefits from (non-vacuous) tight generalization bounds, in a series of numerical experiments when compared to competing algorithms which also minimize PAC-Bayes objectives -- both with uninformed (data-independent) and informed (data-dependent) priors.
Self-Bounding Majority Vote Learning Algorithms by the Direct Minimization of a Tight PAC-Bayesian C-Bound
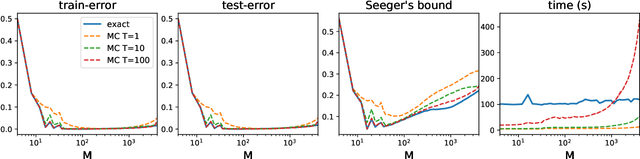
Apr 28, 2021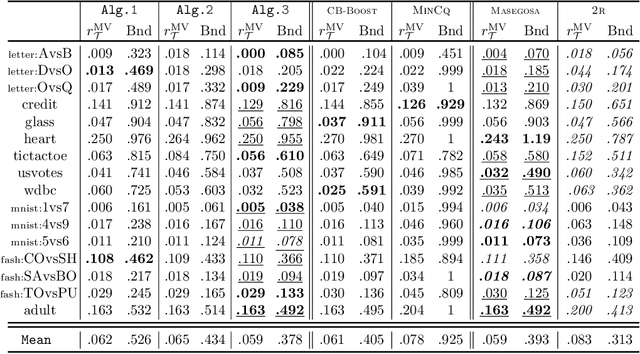
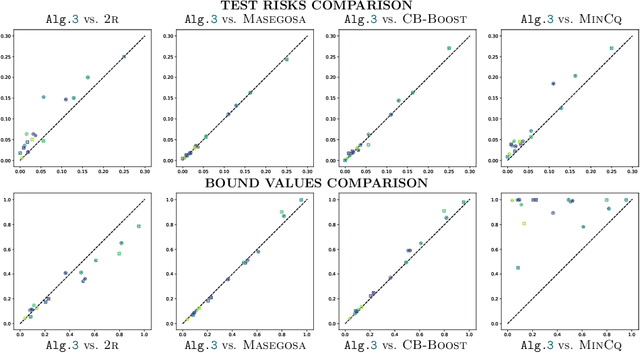

Abstract:In the PAC-Bayesian literature, the C-Bound refers to an insightful relation between the risk of a majority vote classifier (under the zero-one loss) and the first two moments of its margin (i.e., the expected margin and the voters' diversity). Until now, learning algorithms developed in this framework minimize the empirical version of the C-Bound, instead of explicit PAC-Bayesian generalization bounds. In this paper, by directly optimizing PAC-Bayesian guarantees on the C-Bound, we derive self-bounding majority vote learning algorithms. Moreover, our algorithms based on gradient descent are scalable and lead to accurate predictors paired with non-vacuous guarantees.
A PAC-Bayes Analysis of Adversarial Robustness
Feb 19, 2021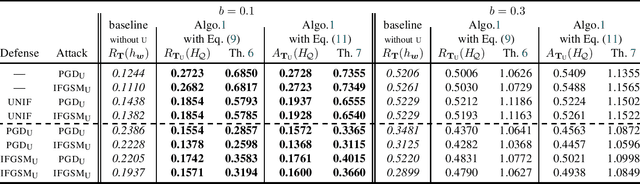
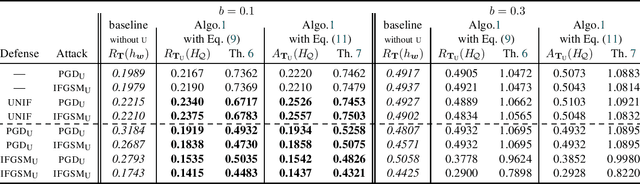
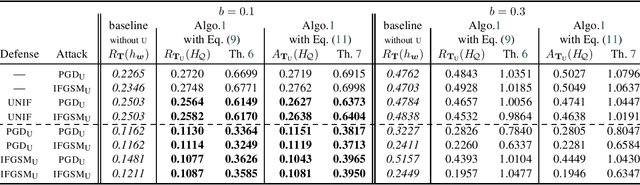
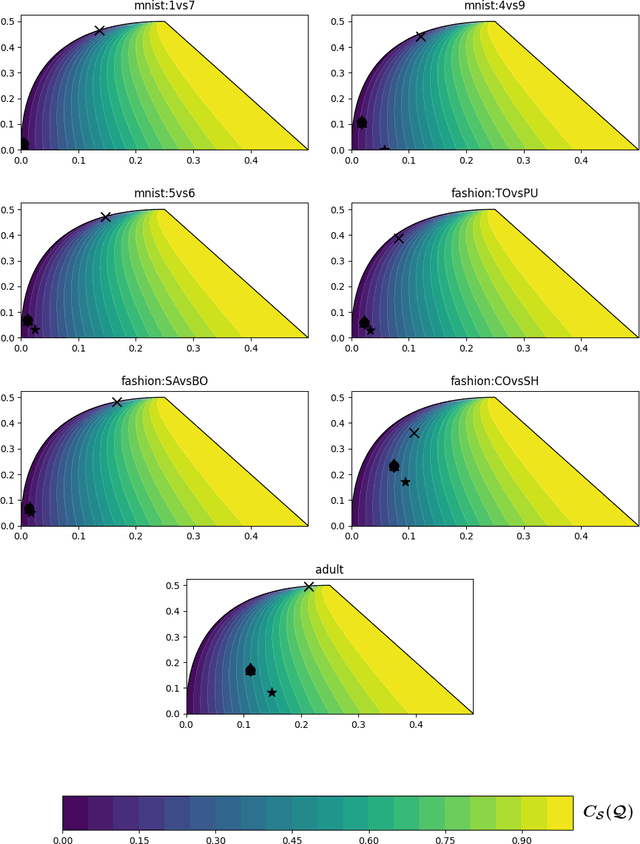
Abstract:We propose the first general PAC-Bayesian generalization bounds for adversarial robustness, that estimate, at test time, how much a model will be invariant to imperceptible perturbations in the input. Instead of deriving a worst-case analysis of the risk of a hypothesis over all the possible perturbations, we leverage the PAC-Bayesian framework to bound the averaged risk on the perturbations for majority votes (over the whole class of hypotheses). Our theoretically founded analysis has the advantage to provide general bounds (i) independent from the type of perturbations (i.e., the adversarial attacks), (ii) that are tight thanks to the PAC-Bayesian framework, (iii) that can be directly minimized during the learning phase to obtain a robust model on different attacks at test time.
A General Framework for the Derandomization of PAC-Bayesian Bounds
Feb 17, 2021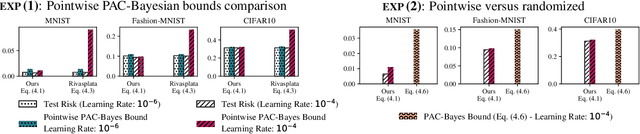
Abstract:PAC-Bayesian bounds are known to be tight and informative when studying the generalization ability of randomized classifiers. However, when applied to some family of deterministic models such as neural networks, they require a loose and costly derandomization step. As an alternative to this step, we introduce three new PAC-Bayesian generalization bounds that have the originality to be pointwise, meaning that they provide guarantees over one single hypothesis instead of the usual averaged analysis. Our bounds are rather general, potentially parameterizable, and provide novel insights for various machine learning settings that rely on randomized algorithms. We illustrate the interest of our theoretical result for the analysis of neural network training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge