A General Framework for the Derandomization of PAC-Bayesian Bounds
Paper and Code
Feb 17, 2021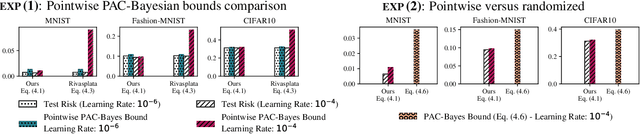
PAC-Bayesian bounds are known to be tight and informative when studying the generalization ability of randomized classifiers. However, when applied to some family of deterministic models such as neural networks, they require a loose and costly derandomization step. As an alternative to this step, we introduce three new PAC-Bayesian generalization bounds that have the originality to be pointwise, meaning that they provide guarantees over one single hypothesis instead of the usual averaged analysis. Our bounds are rather general, potentially parameterizable, and provide novel insights for various machine learning settings that rely on randomized algorithms. We illustrate the interest of our theoretical result for the analysis of neural network training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge