Geometry-Aware Edge Pooling for Graph Neural Networks

Graph Neural Networks (GNNs) have shown significant success for graph-based tasks. Motivated by the prevalence of large datasets in real-world applications, pooling layers are crucial components of GNNs. By reducing the size of input graphs, pooling enables faster training and potentially better generalisation. However, existing pooling operations often optimise for the learning task at the expense of fundamental graph structures and interpretability. This leads to unreliable performance across varying dataset types, downstream tasks and pooling ratios. Addressing these concerns, we propose novel graph pooling layers for structure aware pooling via edge collapses. Our methods leverage diffusion geometry and iteratively reduce a graph's size while preserving both its metric structure and structural diversity. We guide pooling using magnitude, an isometry-invariant diversity measure, which permits us to control the fidelity of the pooling process. Further, we use the spread of a metric space as a faster and more stable alternative ensuring computational efficiency. Empirical results demonstrate that our methods (i) achieve superior performance compared to alternative pooling layers across a range of diverse graph classification tasks, (ii) preserve key spectral properties of the input graphs, and (iii) retain high accuracy across varying pooling ratios.

Metric Space Magnitude for Evaluating Unsupervised Representation Learning

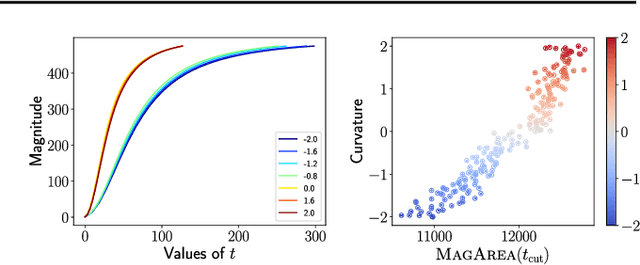
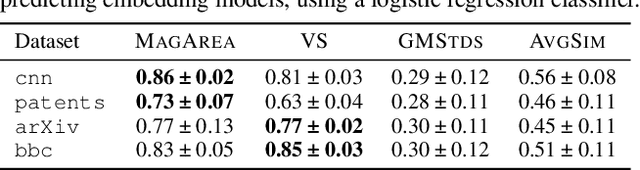
The magnitude of a metric space was recently established as a novel invariant, providing a measure of the `effective size' of a space across multiple scales. By capturing both geometrical and topological properties of data, magnitude is poised to address challenges in unsupervised representation learning tasks. We formalise a novel notion of dissimilarity between magnitude functions of finite metric spaces and use them to derive a quality measure for dimensionality reduction tasks. Our measure is provably stable under perturbations of the data, can be efficiently calculated, and enables a rigorous multi-scale comparison of embeddings. We show the utility of our measure in an experimental suite that comprises different domains and tasks, including the comparison of data visualisations.

Metric Space Magnitude and Generalisation in Neural Networks

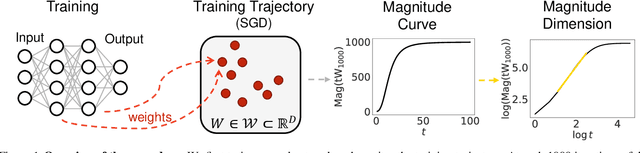
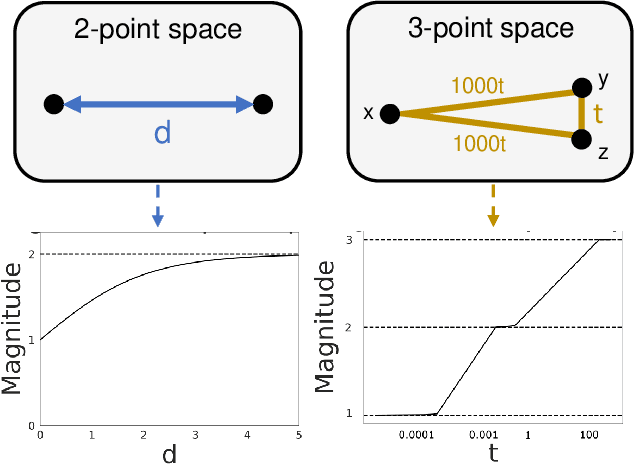
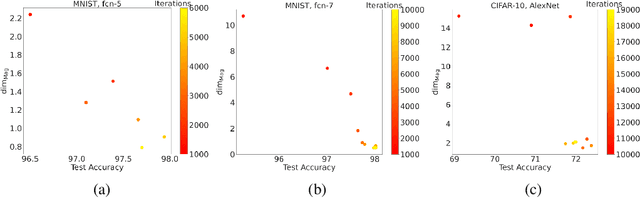
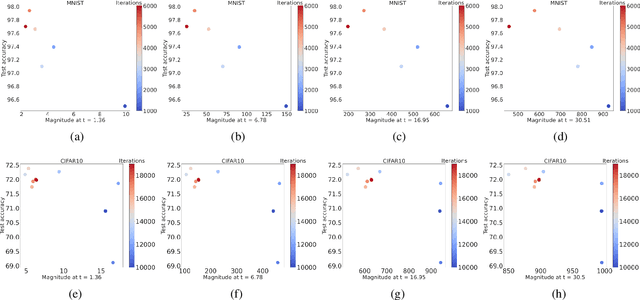
Deep learning models have seen significant successes in numerous applications, but their inner workings remain elusive. The purpose of this work is to quantify the learning process of deep neural networks through the lens of a novel topological invariant called magnitude. Magnitude is an isometry invariant; its properties are an active area of research as it encodes many known invariants of a metric space. We use magnitude to study the internal representations of neural networks and propose a new method for determining their generalisation capabilities. Moreover, we theoretically connect magnitude dimension and the generalisation error, and demonstrate experimentally that the proposed framework can be a good indicator of the latter.