SPITE: Simple Polyhedral Intersection Techniques for modified Environments

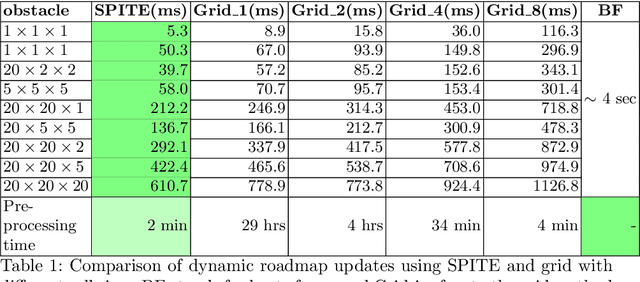
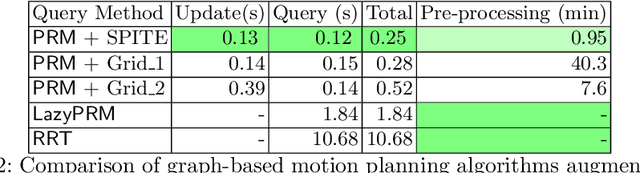
Motion planning in modified environments is a challenging task, as it compounds the innate difficulty of the motion planning problem with a changing environment. This renders some algorithmic methods such as probabilistic roadmaps less viable, as nodes and edges may become invalid as a result of these changes. In this paper, we present a method of transforming any configuration space graph, such as a roadmap, to a dynamic data structure capable of updating the validity of its nodes and edges in response to discrete changes in obstacle positions. We use methods from computational geometry to compute 3D swept volume approximations of configuration space points and curves to achieve 10-40 percent faster updates and up to 60 percent faster motion planning queries than previous algorithms while requiring a significantly shorter pre-processing phase, requiring minutes instead of hours needed by the competing method to achieve somewhat similar update times.

Sampling a Near Neighbor in High Dimensions -- Who is the Fairest of Them All?

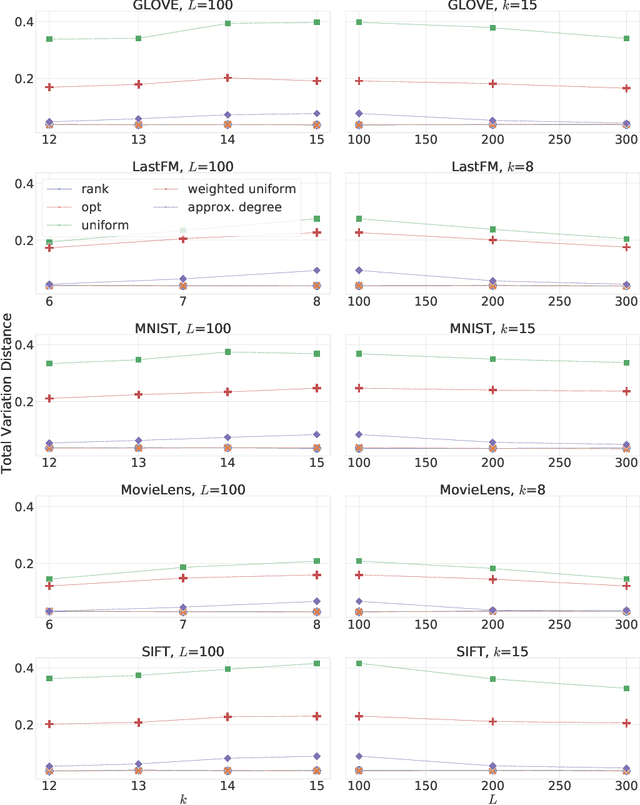
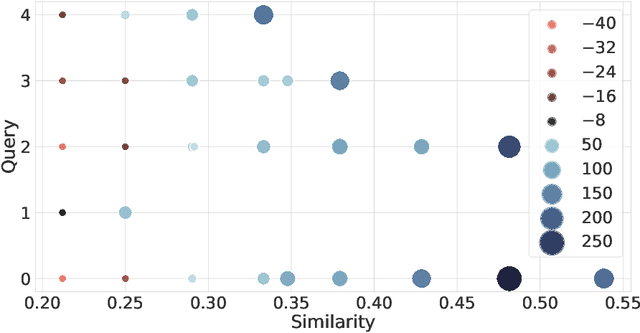
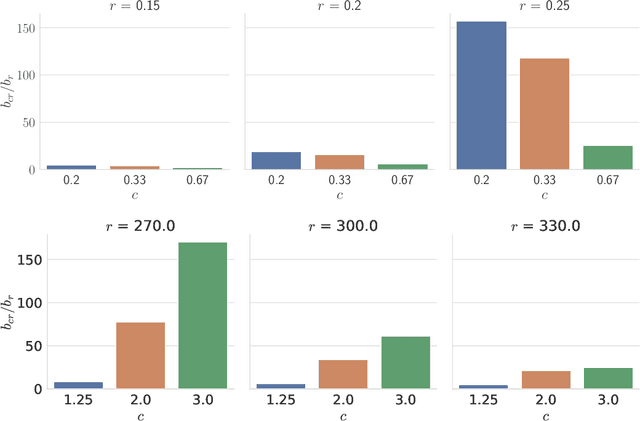
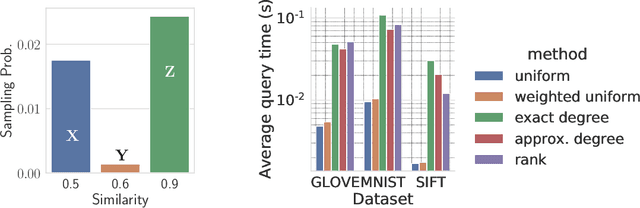
Similarity search is a fundamental algorithmic primitive, widely used in many computer science disciplines. Given a set of points $S$ and a radius parameter $r>0$, the $r$-near neighbor ($r$-NN) problem asks for a data structure that, given any query point $q$, returns a point $p$ within distance at most $r$ from $q$. In this paper, we study the $r$-NN problem in the light of individual fairness and providing equal opportunities: all points that are within distance $r$ from the query should have the same probability to be returned. In the low-dimensional case, this problem was first studied by Hu, Qiao, and Tao (PODS 2014). Locality sensitive hashing (LSH), the theoretically strongest approach to similarity search in high dimensions, does not provide such a fairness guarantee. In this work, we show that LSH based algorithms can be made fair, without a significant loss in efficiency. We propose several efficient data structures for the exact and approximate variants of the fair NN problem. Our approach works more generally for sampling uniformly from a sub-collection of sets of a given collection and can be used in a few other applications. We also develop a data structure for fair similarity search under inner product that requires nearly-linear space and exploits locality sensitive filters. The paper concludes with an experimental evaluation that highlights the inherent unfairness of NN data structures and shows the performance of our algorithms on real-world datasets.

Near Neighbor: Who is the Fairest of Them All?

$\newcommand{\ball}{\mathbb{B}}\newcommand{\dsQ}{{\mathcal{Q}}}\newcommand{\dsS}{{\mathcal{S}}}$In this work we study a fair variant of the near neighbor problem. Namely, given a set of $n$ points $P$ and a parameter $r$, the goal is to preprocess the points, such that given a query point $q$, any point in the $r$-neighborhood of the query, i.e., $\ball(q,r)$, have the same probability of being reported as the near neighbor. We show that LSH based algorithms can be made fair, without a significant loss in efficiency. Specifically, we show an algorithm that reports a point in the $r$-neighborhood of a query $q$ with almost uniform probability. The query time is proportional to $O\bigl( \mathrm{dns}(q.r) \dsQ(n,c) \bigr)$, and its space is $O(\dsS(n,c))$, where $\dsQ(n,c)$ and $\dsS(n,c)$ are the query time and space of an LSH algorithm for $c$-approximate near neighbor, and $\mathrm{dns}(q,r)$ is a function of the local density around $q$. Our approach works more generally for sampling uniformly from a sub-collection of sets of a given collection and can be used in a few other applications. Finally, we run experiments to show performance of our approach on real data.

Sparse Approximation via Generating Point Sets

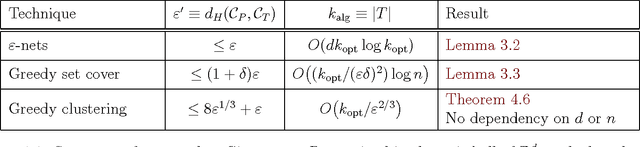
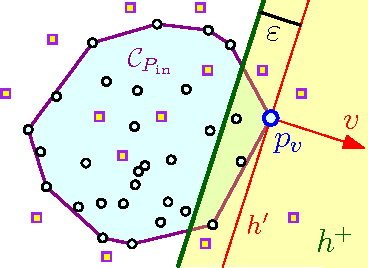
$ \newcommand{\kalg}{{k_{\mathrm{alg}}}} \newcommand{\kopt}{{k_{\mathrm{opt}}}} \newcommand{\algset}{{T}} \renewcommand{\Re}{\mathbb{R}} \newcommand{\eps}{\varepsilon} \newcommand{\pth}[2][\!]{#1\left({#2}\right)} \newcommand{\npoints}{n} \newcommand{\ballD}{\mathsf{b}} \newcommand{\dataset}{{P}} $ For a set $\dataset$ of $\npoints$ points in the unit ball $\ballD \subseteq \Re^d$, consider the problem of finding a small subset $\algset \subseteq \dataset$ such that its convex-hull $\eps$-approximates the convex-hull of the original set. We present an efficient algorithm to compute such a $\eps'$-approximation of size $\kalg$, where $\eps'$ is function of $\eps$, and $\kalg$ is a function of the minimum size $\kopt$ of such an $\eps$-approximation. Surprisingly, there is no dependency on the dimension $d$ in both bounds. Furthermore, every point of $\dataset$ can be $\eps$-approximated by a convex-combination of points of $\algset$ that is $O(1/\eps^2)$-sparse. Our result can be viewed as a method for sparse, convex autoencoding: approximately representing the data in a compact way using sparse combinations of a small subset $\algset$ of the original data. The new algorithm can be kernelized, and it preserves sparsity in the original input.

A Simple Algorithm for Maximum Margin Classification, Revisited

In this note, we revisit the algorithm of Har-Peled et. al. [HRZ07] for computing a linear maximum margin classifier. Our presentation is self contained, and the algorithm itself is slightly simpler than the original algorithm. The algorithm itself is a simple Perceptron like iterative algorithm. For more details and background, the reader is referred to the original paper.