A Survey on Design Methodologies for Accelerating Deep Learning on Heterogeneous Architectures

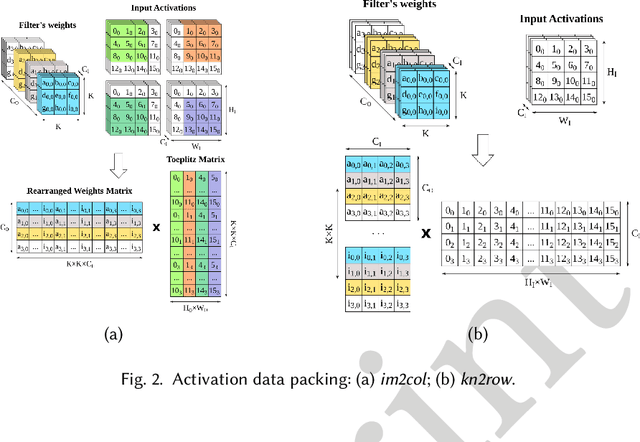
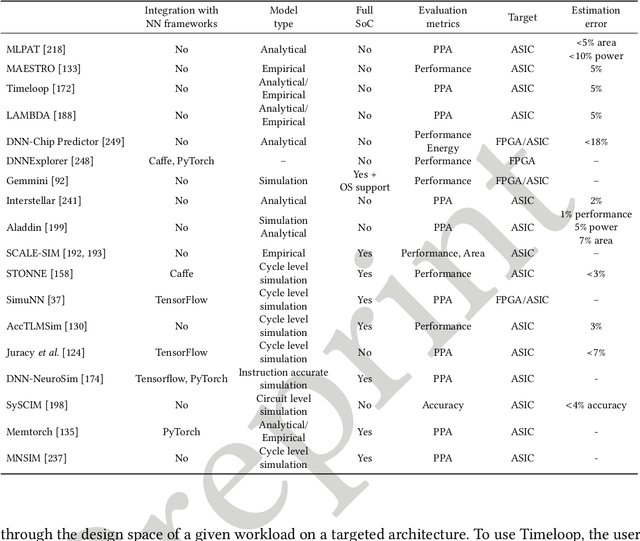
In recent years, the field of Deep Learning has seen many disruptive and impactful advancements. Given the increasing complexity of deep neural networks, the need for efficient hardware accelerators has become more and more pressing to design heterogeneous HPC platforms. The design of Deep Learning accelerators requires a multidisciplinary approach, combining expertise from several areas, spanning from computer architecture to approximate computing, computational models, and machine learning algorithms. Several methodologies and tools have been proposed to design accelerators for Deep Learning, including hardware-software co-design approaches, high-level synthesis methods, specific customized compilers, and methodologies for design space exploration, modeling, and simulation. These methodologies aim to maximize the exploitable parallelism and minimize data movement to achieve high performance and energy efficiency. This survey provides a holistic review of the most influential design methodologies and EDA tools proposed in recent years to implement Deep Learning accelerators, offering the reader a wide perspective in this rapidly evolving field. In particular, this work complements the previous survey proposed by the same authors in [203], which focuses on Deep Learning hardware accelerators for heterogeneous HPC platforms.

On the Bike Spreading Problem

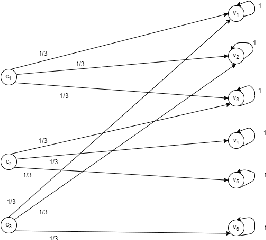
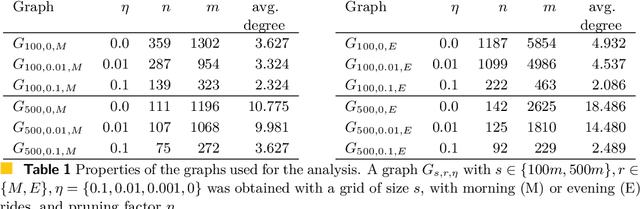
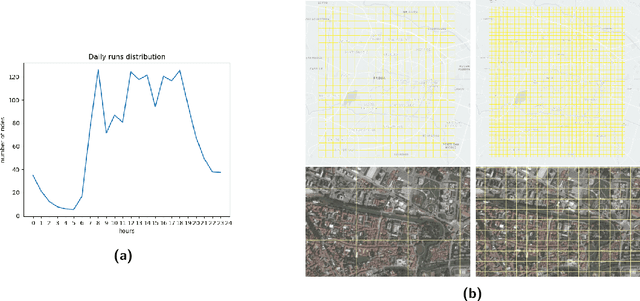
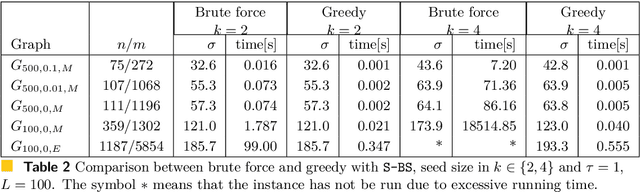
A free-floating bike-sharing system (FFBSS) is a dockless rental system where an individual can borrow a bike and returns it everywhere, within the service area. To improve the rental service, available bikes should be distributed over the entire service area: a customer leaving from any position is then more likely to find a near bike and then to use the service. Moreover, spreading bikes among the entire service area increases urban spatial equity since the benefits of FFBSS are not a prerogative of just a few zones. For guaranteeing such distribution, the FFBSS operator can use vans to manually relocate bikes, but it incurs high economic and environmental costs. We propose a novel approach that exploits the existing bike flows generated by customers to distribute bikes. More specifically, by envisioning the problem as an Influence Maximization problem, we show that it is possible to position batches of bikes on a small number of zones, and then the daily use of FFBSS will efficiently spread these bikes on a large area. We show that detecting these areas is NP-complete, but there exists a simple and efficient $1-1/e$ approximation algorithm; our approach is then evaluated on a dataset of rides from the free-floating bike-sharing system of the city of Padova.

Sampling a Near Neighbor in High Dimensions -- Who is the Fairest of Them All?

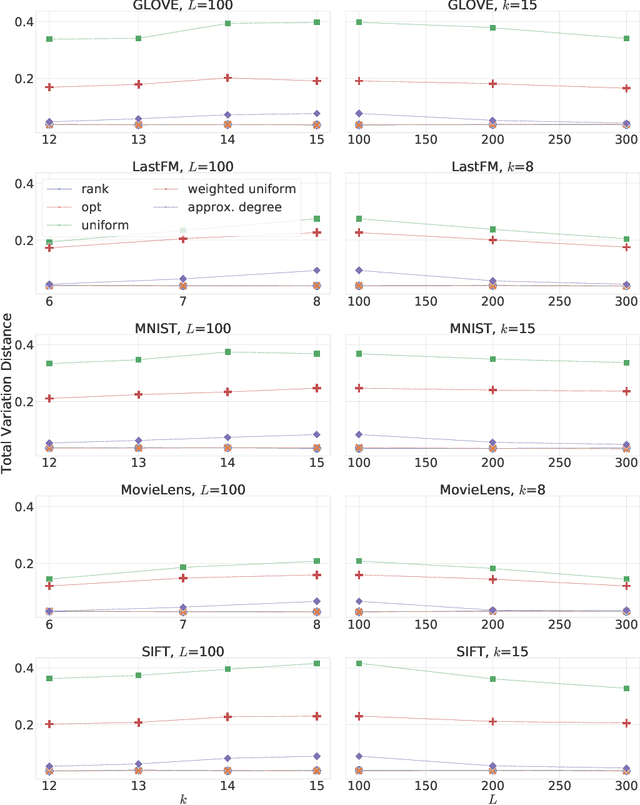
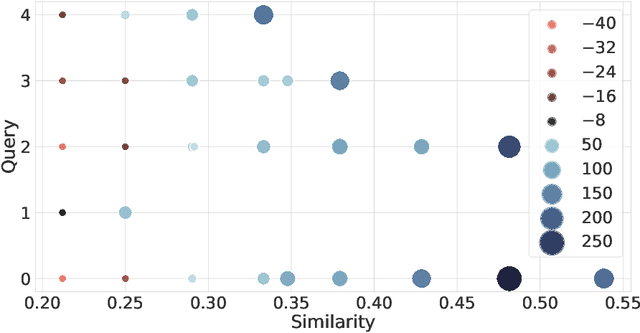
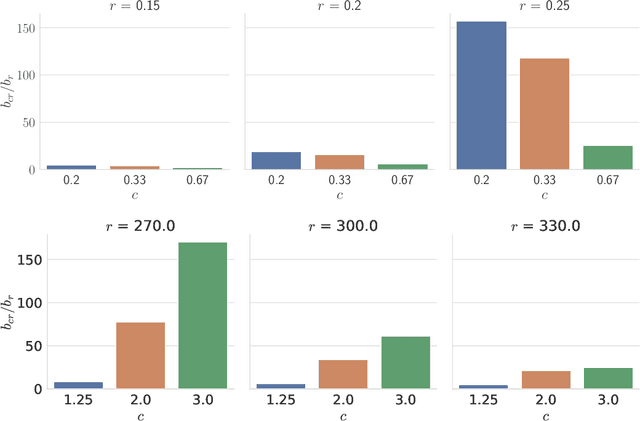
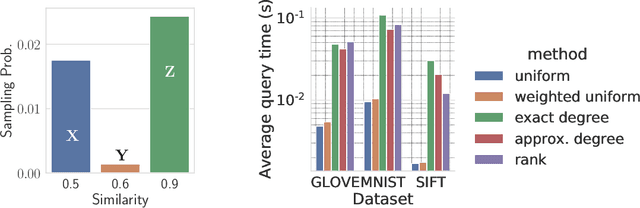
Similarity search is a fundamental algorithmic primitive, widely used in many computer science disciplines. Given a set of points $S$ and a radius parameter $r>0$, the $r$-near neighbor ($r$-NN) problem asks for a data structure that, given any query point $q$, returns a point $p$ within distance at most $r$ from $q$. In this paper, we study the $r$-NN problem in the light of individual fairness and providing equal opportunities: all points that are within distance $r$ from the query should have the same probability to be returned. In the low-dimensional case, this problem was first studied by Hu, Qiao, and Tao (PODS 2014). Locality sensitive hashing (LSH), the theoretically strongest approach to similarity search in high dimensions, does not provide such a fairness guarantee. In this work, we show that LSH based algorithms can be made fair, without a significant loss in efficiency. We propose several efficient data structures for the exact and approximate variants of the fair NN problem. Our approach works more generally for sampling uniformly from a sub-collection of sets of a given collection and can be used in a few other applications. We also develop a data structure for fair similarity search under inner product that requires nearly-linear space and exploits locality sensitive filters. The paper concludes with an experimental evaluation that highlights the inherent unfairness of NN data structures and shows the performance of our algorithms on real-world datasets.

A Computational Model for Tensor Core Units

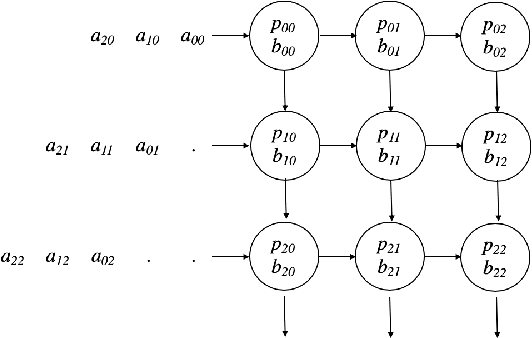
To respond to the need of efficient training and inference of deep neural networks, a pletora of domain-specific hardware architectures have been introduced, such as Google Tensor Processing Units and NVIDIA Tensor Cores. A common feature of these architectures is a hardware circuit for efficiently computing a dense matrix multiplication of a given small size. In order to broad the class of algorithms that exploit these systems, we propose a computational model, named TCU model, that captures the ability to natively multiply small matrices. We then use the TCU model for designing fast algorithms for linear algebra problems, including dense and sparse matrix multiplication, FFT, integer multiplication, and polynomial evaluation. We finally highlight a relation between the TCU model and the external memory model.

Fair Near Neighbor Search: Independent Range Sampling in High Dimensions

Similarity search is a fundamental algorithmic primitive, widely used in many computer science disciplines. There are several variants of the similarity search problem, and one of the most relevant is the $r$-near neighbor ($r$-NN) problem: given a radius $r>0$ and a set of points $S$, construct a data structure that, for any given query point $q$, returns a point $p$ within distance at most $r$ from $q$. In this paper, we study the $r$-NN problem in the light of fairness. We consider fairness in the sense of equal opportunity: all points that are within distance $r$ from the query should have the same probability to be returned. Locality sensitive hashing (LSH), the most common approach to similarity search in high dimensions, does not provide such a fairness guarantee. To address this, we propose efficient data structures for $r$-NN where all points in $S$ that are near $q$ have the same probability to be selected and returned by the query. Specifically, we first propose a black-box approach that, given any LSH scheme, constructs a data structure for uniformly sampling points in the neighborhood of a query. Then, we develop a data structure for fair similarity search under inner product, which requires nearly-linear space and exploits locality sensitive filters.

Symmetry-free SDP Relaxations for Affine Subspace Clustering

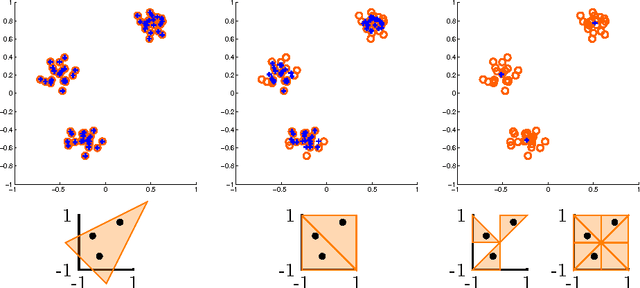
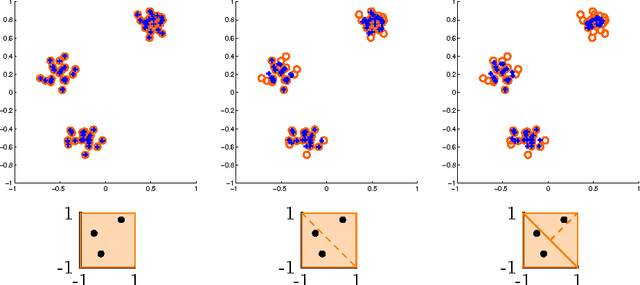
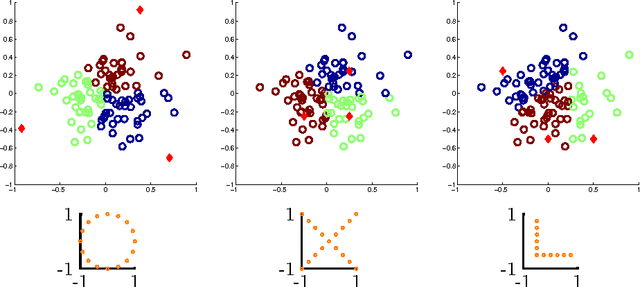
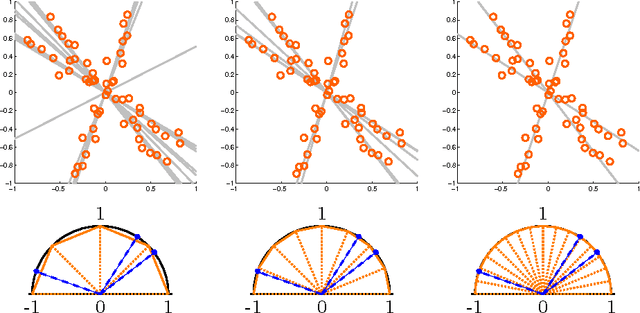
We consider clustering problems where the goal is to determine an optimal partition of a given point set in Euclidean space in terms of a collection of affine subspaces. While there is vast literature on heuristics for this kind of problem, such approaches are known to be susceptible to poor initializations and getting trapped in bad local optima. We alleviate these issues by introducing a semidefinite relaxation based on Lasserre's method of moments. While a similiar approach is known for classical Euclidean clustering problems, a generalization to our more general subspace scenario is not straightforward, due to the high symmetry of the objective function that weakens any convex relaxation. We therefore introduce a new mechanism for symmetry breaking based on covering the feasible region with polytopes. Additionally, we introduce and analyze a deterministic rounding heuristic.

On the Complexity of Inner Product Similarity Join

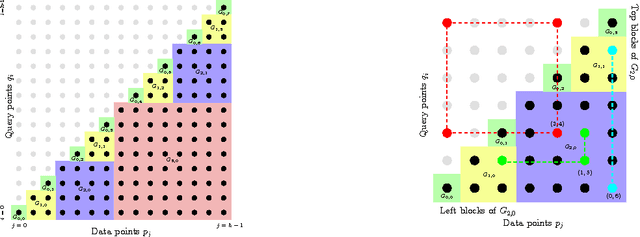
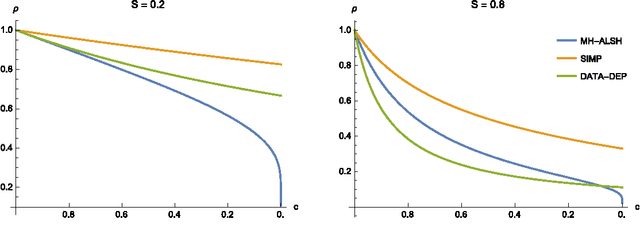
A number of tasks in classification, information retrieval, recommendation systems, and record linkage reduce to the core problem of inner product similarity join (IPS join): identifying pairs of vectors in a collection that have a sufficiently large inner product. IPS join is well understood when vectors are normalized and some approximation of inner products is allowed. However, the general case where vectors may have any length appears much more challenging. Recently, new upper bounds based on asymmetric locality-sensitive hashing (ALSH) and asymmetric embeddings have emerged, but little has been known on the lower bound side. In this paper we initiate a systematic study of inner product similarity join, showing new lower and upper bounds. Our main results are: * Approximation hardness of IPS join in subquadratic time, assuming the strong exponential time hypothesis. * New upper and lower bounds for (A)LSH-based algorithms. In particular, we show that asymmetry can be avoided by relaxing the LSH definition to only consider the collision probability of distinct elements. * A new indexing method for IPS based on linear sketches, implying that our hardness results are not far from being tight. Our technical contributions include new asymmetric embeddings that may be of independent interest. At the conceptual level we strive to provide greater clarity, for example by distinguishing among signed and unsigned variants of IPS join and shedding new light on the effect of asymmetry.