Discrete Potts Model for Generating Superpixels on Noisy Images

Many computer vision applications, such as object recognition and segmentation, increasingly build on superpixels. However, there have been so far few superpixel algorithms that systematically deal with noisy images. We propose to first decompose the image into equal-sized rectangular patches, which also sets the maximum superpixel size. Within each patch, a Potts model for simultaneous segmentation and denoising is applied, that guarantees connected and non-overlapping superpixels and also produces a denoised image. The corresponding optimization problem is formulated as a mixed integer linear program (MILP), and solved by a commercial solver. Extensive experiments on the BSDS500 dataset images with noises are compared with other state-of-the-art superpixel methods. Our method achieves the best result in terms of a combined score (OP) composed of the under-segmentation error, boundary recall and compactness.

An ILP Solver for Multi-label MRFs with Connectivity Constraints

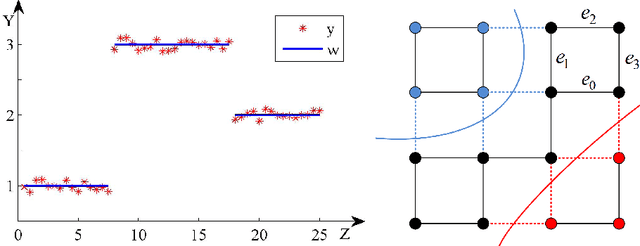
Integer Linear Programming (ILP) formulations of Markov random fields (MRFs) models with global connectivity priors were investigated previously in computer vision, e.g., \cite{globalinter,globalconn}. In these works, only Linear Programing (LP) relaxations \cite{globalinter,globalconn} or simplified versions \cite{graphcutbase} of the problem were solved. This paper investigates the ILP of multi-label MRF with exact connectivity priors via a branch-and-cut method, which provably finds globally optimal solutions. The method enforces connectivity priors iteratively by a cutting plane method, and provides feasible solutions with a guarantee on sub-optimality even if we terminate it earlier. The proposed ILP can be applied as a post-processing method on top of any existing multi-label segmentation approach. As it provides globally optimal solution, it can be used off-line to generate ground-truth labeling, which serves as quality check for any fast on-line algorithm. Furthermore, it can be used to generate ground-truth proposals for weakly supervised segmentation. We demonstrate the power and usefulness of our model by several experiments on the BSDS500 and PASCAL image dataset, as well as on medical images with trained probability maps.

A First Derivative Potts Model for Segmentation and Denoising Using ILP

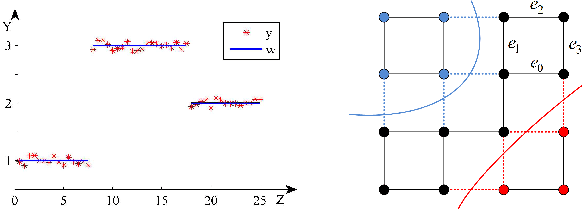
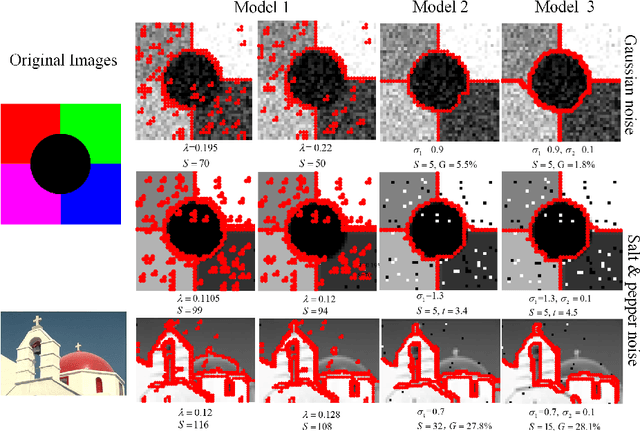
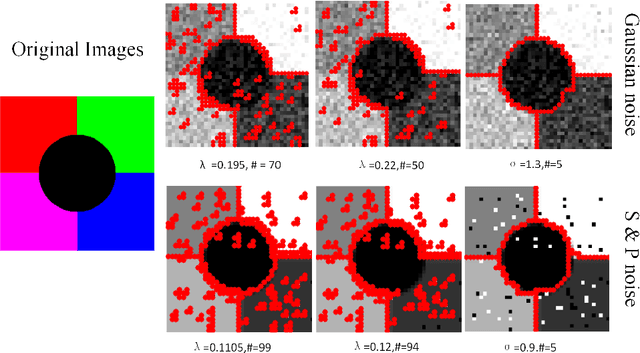
Unsupervised image segmentation and denoising are two fundamental tasks in image processing. Usually, graph based models such as multicut are used for segmentation and variational models are employed for denoising. Our approach addresses both problems at the same time. We propose a novel ILP formulation of the first derivative Potts model with the $\ell_1$ data term, where binary variables are introduced to deal with the $\ell_0$ norm of the regularization term. The ILP is then solved by a standard off-the-shelf MIP solver. Numerical experiments are compared with the multicut problem.

Symmetry-free SDP Relaxations for Affine Subspace Clustering

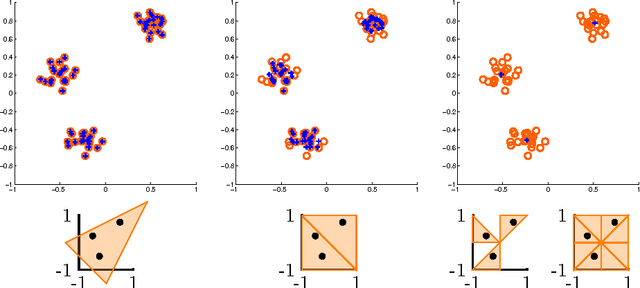
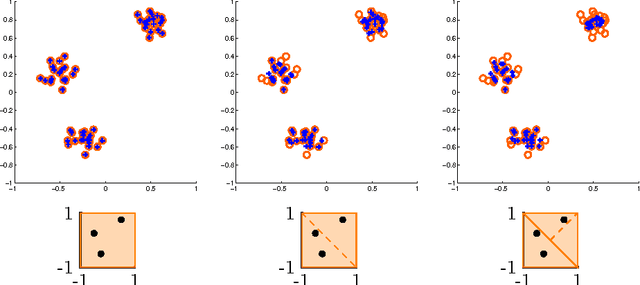
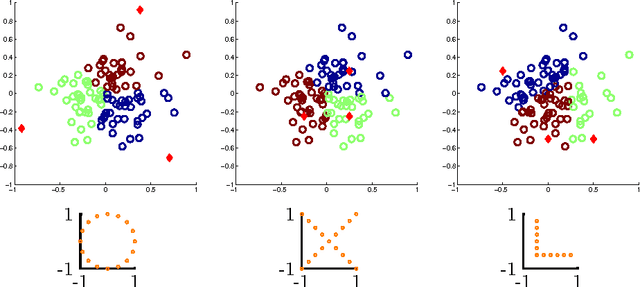
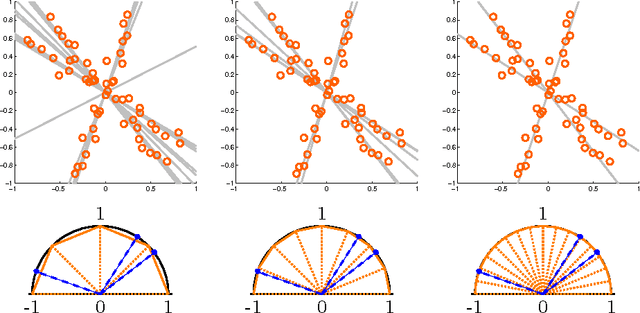
We consider clustering problems where the goal is to determine an optimal partition of a given point set in Euclidean space in terms of a collection of affine subspaces. While there is vast literature on heuristics for this kind of problem, such approaches are known to be susceptible to poor initializations and getting trapped in bad local optima. We alleviate these issues by introducing a semidefinite relaxation based on Lasserre's method of moments. While a similiar approach is known for classical Euclidean clustering problems, a generalization to our more general subspace scenario is not straightforward, due to the high symmetry of the objective function that weakens any convex relaxation. We therefore introduce a new mechanism for symmetry breaking based on covering the feasible region with polytopes. Additionally, we introduce and analyze a deterministic rounding heuristic.

Higher-order Segmentation via Multicuts

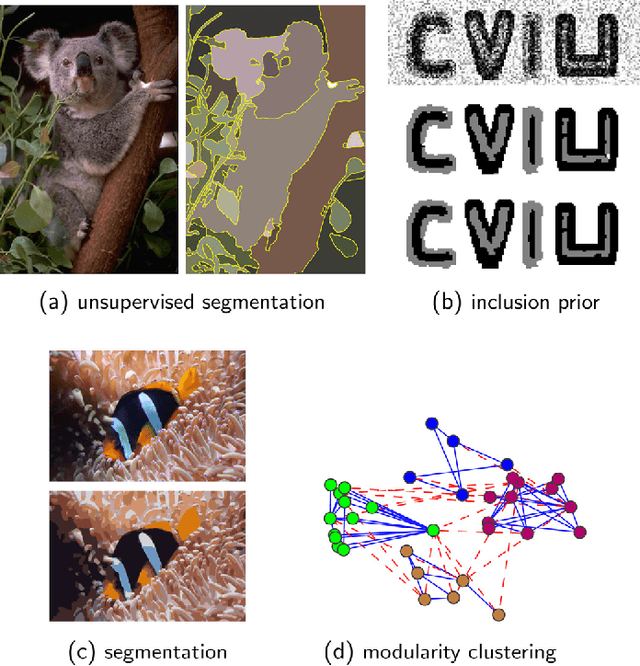
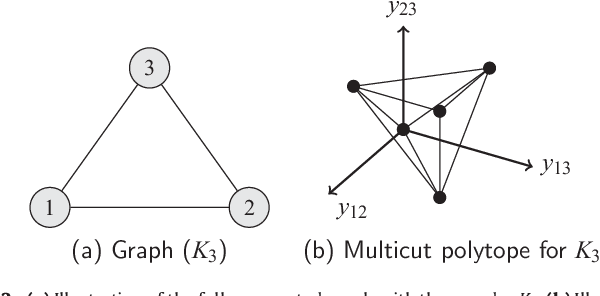
Multicuts enable to conveniently represent discrete graphical models for unsupervised and supervised image segmentation, in the case of local energy functions that exhibit symmetries. The basic Potts model and natural extensions thereof to higher-order models provide a prominent class of such objectives, that cover a broad range of segmentation problems relevant to image analysis and computer vision. We exhibit a way to systematically take into account such higher-order terms for computational inference. Furthermore, we present results of a comprehensive and competitive numerical evaluation of a variety of dedicated cutting-plane algorithms. Our approach enables the globally optimal evaluation of a significant subset of these models, without compromising runtime. Polynomially solvable relaxations are studied as well, along with advanced rounding schemes for post-processing.