Christoph Schnoerr
Higher-order Segmentation via Multicuts
Nov 16, 2015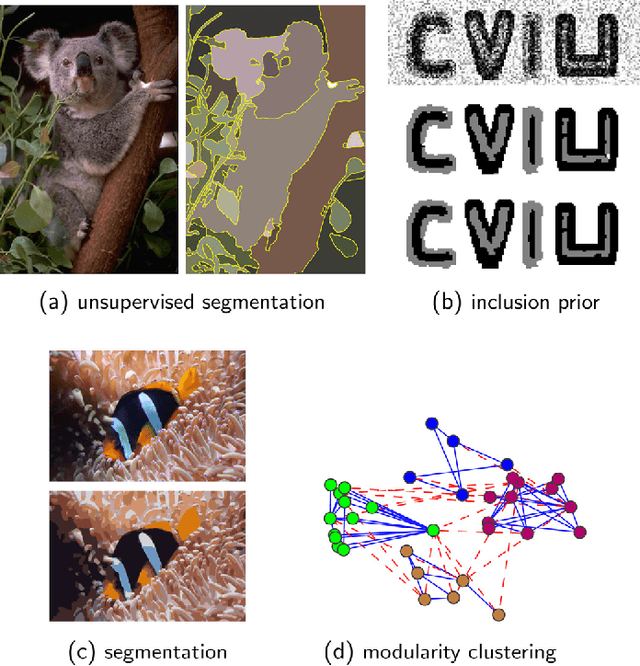


Abstract:Multicuts enable to conveniently represent discrete graphical models for unsupervised and supervised image segmentation, in the case of local energy functions that exhibit symmetries. The basic Potts model and natural extensions thereof to higher-order models provide a prominent class of such objectives, that cover a broad range of segmentation problems relevant to image analysis and computer vision. We exhibit a way to systematically take into account such higher-order terms for computational inference. Furthermore, we present results of a comprehensive and competitive numerical evaluation of a variety of dedicated cutting-plane algorithms. Our approach enables the globally optimal evaluation of a significant subset of these models, without compromising runtime. Polynomially solvable relaxations are studied as well, along with advanced rounding schemes for post-processing.
Efficient MRF Energy Minimization via Adaptive Diminishing Smoothing
Oct 16, 2012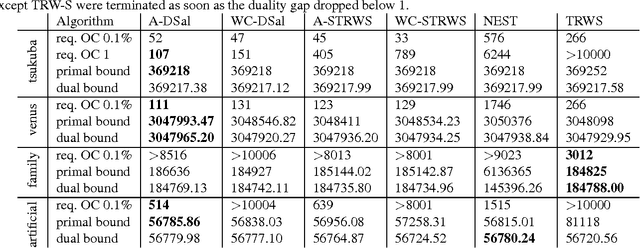

Abstract:We consider the linear programming relaxation of an energy minimization problem for Markov Random Fields. The dual objective of this problem can be treated as a concave and unconstrained, but non-smooth function. The idea of smoothing the objective prior to optimization was recently proposed in a series of papers. Some of them suggested the idea to decrease the amount of smoothing (so called temperature) while getting closer to the optimum. However, no theoretical substantiation was provided. We propose an adaptive smoothing diminishing algorithm based on the duality gap between relaxed primal and dual objectives and demonstrate the efficiency of our approach with a smoothed version of Sequential Tree-Reweighted Message Passing (TRW-S) algorithm. The strategy is applicable to other algorithms as well, avoids adhoc tuning of the smoothing during iterations, and provably guarantees convergence to the optimum.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge