Unlocking the Potential of Operations Research for Multi-Graph Matching

We consider the incomplete multi-graph matching problem, which is a generalization of the NP-hard quadratic assignment problem for matching multiple finite sets. Multi-graph matching plays a central role in computer vision, e.g., for matching images or shapes, so that a number of dedicated optimization techniques have been proposed. While the closely related NP-hard multi-dimensional assignment problem (MDAP) has been studied for decades in the operations research community, it only considers complete matchings and has a different cost structure. We bridge this gap and transfer well-known approximation algorithms for the MDAP to incomplete multi-graph matching. To this end, we revisit respective algorithms, adapt them to incomplete multi-graph matching, and propose their extended and parallelized versions. Our experimental validation shows that our new method substantially outperforms the previous state of the art in terms of objective and runtime. Our algorithm matches, for example, 29 images with more than 500 keypoints each in less than two minutes, whereas the fastest considered competitor requires at least half an hour while producing far worse results.

Unsupervised Deep Graph Matching Based on Cycle Consistency

We contribute to the sparsely populated area of unsupervised deep graph matching with application to keypoint matching in images. Contrary to the standard \emph{supervised} approach, our method does not require ground truth correspondences between keypoint pairs. Instead, it is self-supervised by enforcing consistency of matchings between images of the same object category. As the matching and the consistency loss are discrete, their derivatives cannot be straightforwardly used for learning. We address this issue in a principled way by building our method upon the recent results on black-box differentiation of combinatorial solvers. This makes our method exceptionally flexible, as it is compatible with arbitrary network architectures and combinatorial solvers. Our experimental evaluation suggests that our technique sets a new state-of-the-art for unsupervised graph matching.

Relative-Interior Solution for (Incomplete) Linear Assignment Problem with Applications to Quadratic Assignment Problem

We study the set of optimal solutions of the dual linear programming formulation of the linear assignment problem (LAP) to propose a method for computing a solution from the relative interior of this set. Assuming that an arbitrary dual-optimal solution and an optimal assignment are available (for which many efficient algorithms already exist), our method computes a relative-interior solution in linear time. Since LAP occurs as a subproblem in the linear programming relaxation of quadratic assignment problem (QAP), we employ our method as a new component in the family of dual-ascent algorithms that provide bounds on the optimal value of QAP. To make our results applicable to incomplete QAP, which is of interest in practical use-cases, we also provide a linear-time reduction from incomplete LAP to complete LAP along with a mapping that preserves optimality and membership in the relative interior. Our experiments on publicly available benchmarks indicate that our approach with relative-interior solution is frequently capable of providing superior bounds and otherwise is at least comparable.

A Comparative Study of Graph Matching Algorithms in Computer Vision

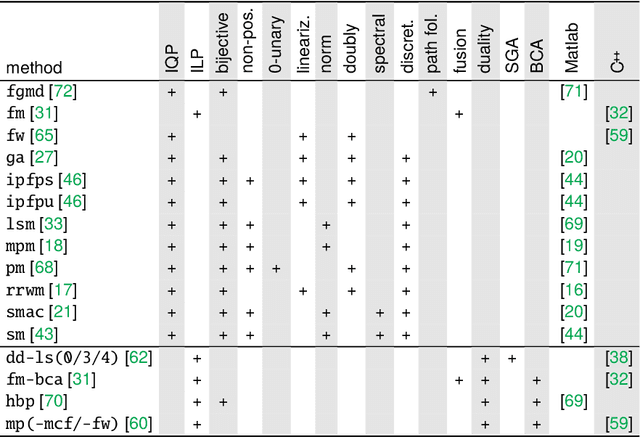
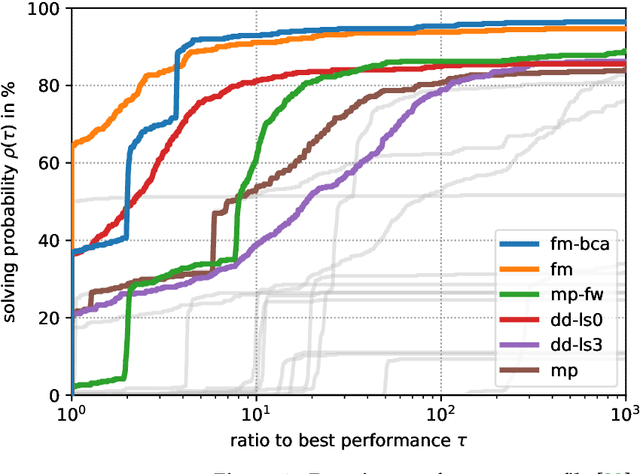
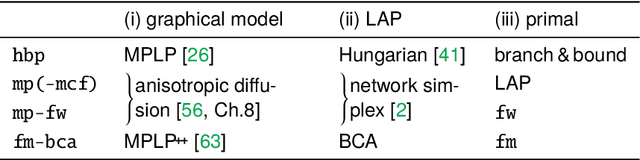
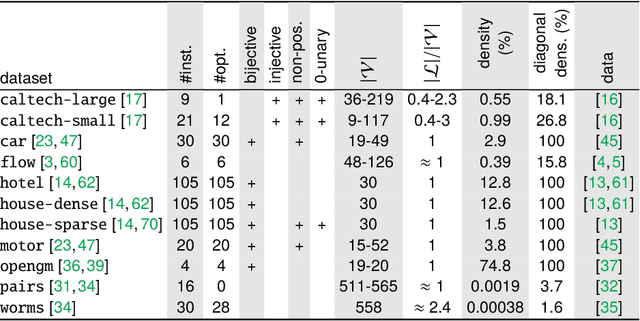
The graph matching optimization problem is an essential component for many tasks in computer vision, such as bringing two deformable objects in correspondence. Naturally, a wide range of applicable algorithms have been proposed in the last decades. Since a common standard benchmark has not been developed, their performance claims are often hard to verify as evaluation on differing problem instances and criteria make the results incomparable. To address these shortcomings, we present a comparative study of graph matching algorithms. We create a uniform benchmark where we collect and categorize a large set of existing and publicly available computer vision graph matching problems in a common format. At the same time we collect and categorize the most popular open-source implementations of graph matching algorithms. Their performance is evaluated in a way that is in line with the best practices for comparing optimization algorithms. The study is designed to be reproducible and extensible to serve as a valuable resource in the future. Our study provides three notable insights: 1.) popular problem instances are exactly solvable in substantially less than 1 second and, therefore, are insufficient for future empirical evaluations; 2.) the most popular baseline methods are highly inferior to the best available methods; 3.) despite the NP-hardness of the problem, instances coming from vision applications are often solvable in a few seconds even for graphs with more than 500 vertices.

Fusion Moves for Graph Matching

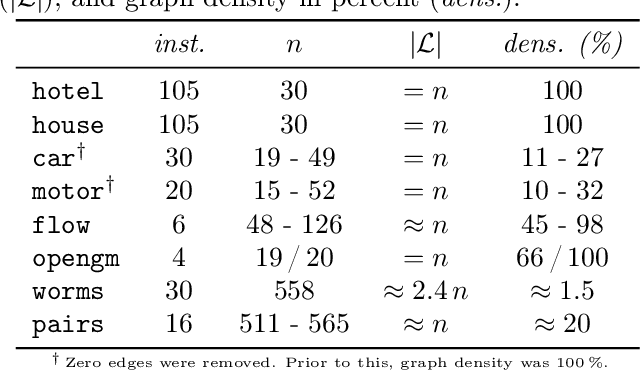
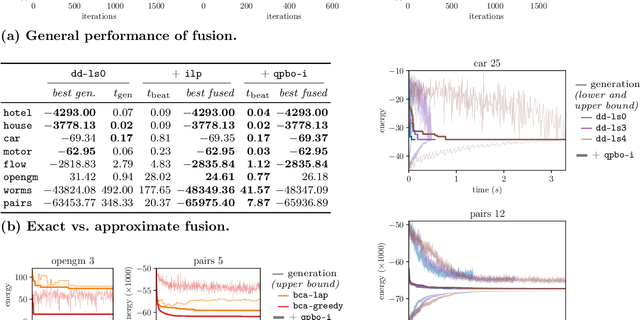
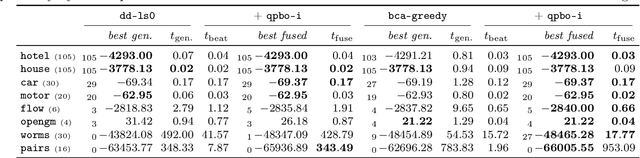
We contribute to approximate algorithms for the quadratic assignment problem also known as graph matching. Inspired by the success of the fusion moves technique developed for multilabel discrete Markov random fields, we investigate its applicability to graph matching. In particular, we show how it can be efficiently combined with the dedicated state-of-the-art Lagrange dual methods that have recently shown superior results in computer vision and bio-imaging applications. As our empirical evaluation on a wide variety of graph matching datasets suggests, fusion moves notably improve performance of these methods in terms of speed and quality of the obtained solutions. Hence, this combination results in a state-of-the-art solver for graph matching.

MPLP++: Fast, Parallel Dual Block-Coordinate Ascent for Dense Graphical Models

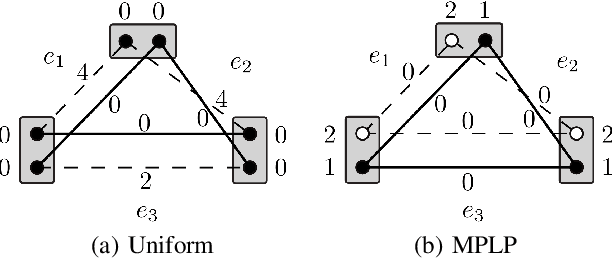
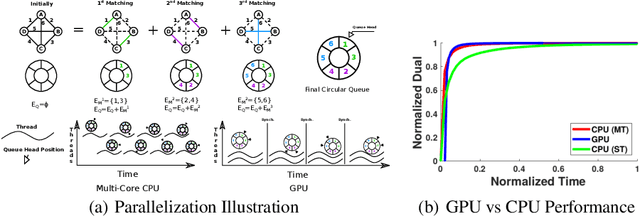
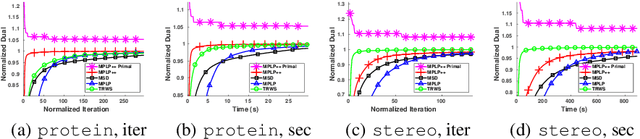
Dense, discrete Graphical Models with pairwise potentials are a powerful class of models which are employed in state-of-the-art computer vision and bio-imaging applications. This work introduces a new MAP-solver, based on the popular Dual Block-Coordinate Ascent principle. Surprisingly, by making a small change to the low-performing solver, the Max Product Linear Programming (MPLP) algorithm, we derive the new solver MPLP++ that significantly outperforms all existing solvers by a large margin, including the state-of-the-art solver Tree-Reweighted Sequential (TRWS) message-passing algorithm. Additionally, our solver is highly parallel, in contrast to TRWS, which gives a further boost in performance with the proposed GPU and multi-thread CPU implementations. We verify the superiority of our algorithm on dense problems from publicly available benchmarks, as well, as a new benchmark for 6D Object Pose estimation. We also provide an ablation study with respect to graph density.

Taxonomy of Dual Block-Coordinate Ascent Methods for Discrete Energy Minimization

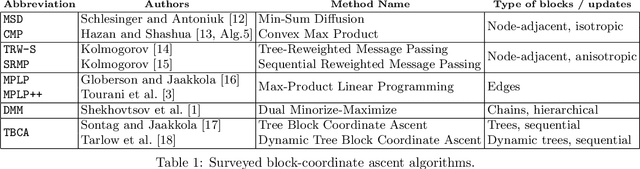
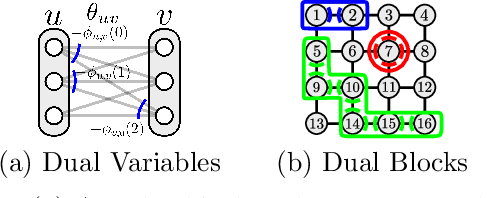
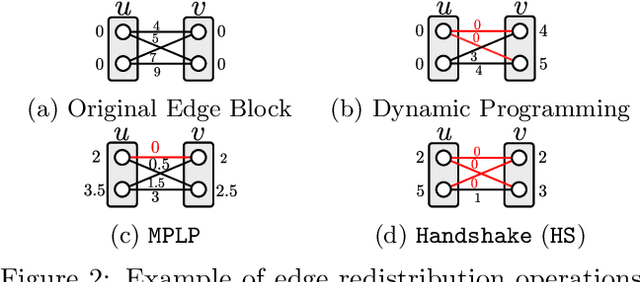
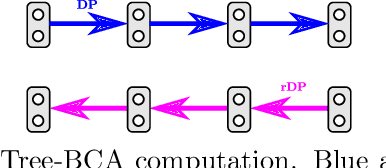
We consider the maximum-a-posteriori inference problem in discrete graphical models and study solvers based on the dual block-coordinate ascent rule. We map all existing solvers in a single framework, allowing for a better understanding of their design principles. We theoretically show that some block-optimizing updates are sub-optimal and how to strictly improve them. On a wide range of problem instances of varying graph connectivity, we study the performance of existing solvers as well as new variants that can be obtained within the framework. As a result of this exploration we build a new state-of-the art solver, performing uniformly better on the whole range of test instances.

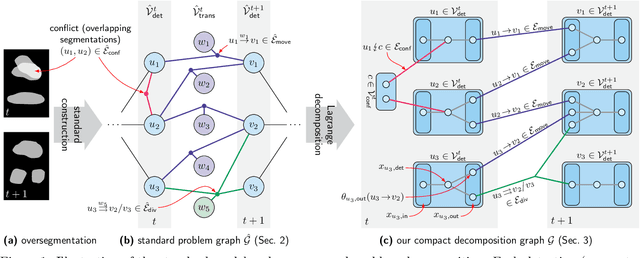
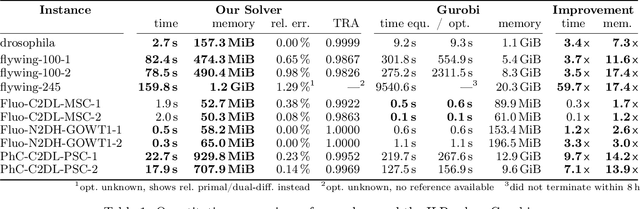
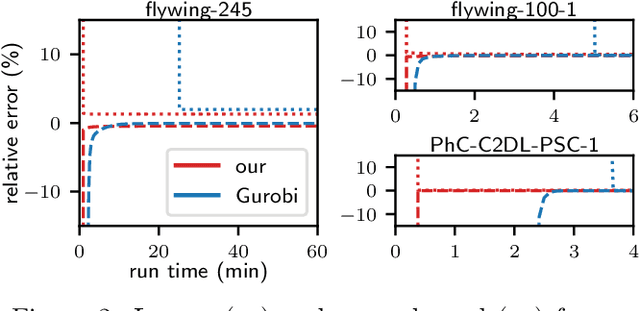
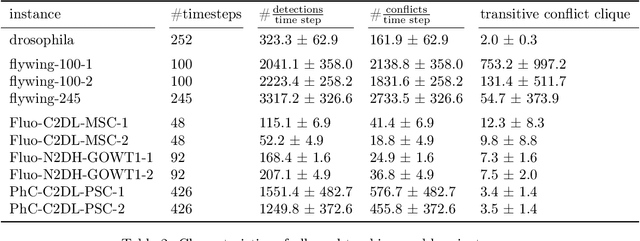
A Primal-Dual Solver for Large-Scale Tracking-by-Assignment

We propose a fast approximate solver for the combinatorial problem known as tracking-by-assignment, which we apply to cell tracking. The latter plays a key role in discovery in many life sciences, especially in cell and developmental biology. So far, in the most general setting this problem was addressed by off-the-shelf solvers like Gurobi, whose run time and memory requirements rapidly grow with the size of the input. In contrast, for our method this growth is nearly linear. Our contribution consists of a new (1) decomposable compact representation of the problem; (2) dual block-coordinate ascent method for optimizing the decomposition-based dual; and (3) primal heuristics that reconstructs a feasible integer solution based on the dual information. Compared to solving the problem with Gurobi, we observe an up to~60~times speed-up, while reducing the memory footprint significantly. We demonstrate the efficacy of our method on real-world tracking problems.

Exact MAP-Inference by Confining Combinatorial Search with LP Relaxation

We consider the MAP-inference problem for graphical models, which is a valued constraint satisfaction problem defined on real numbers with a natural summation operation. We propose a family of relaxations (different from the famous Sherali-Adams hierarchy), which naturally define lower bounds for its optimum. This family always contains a tight relaxation and we give an algorithm able to find it and therefore, solve the initial non-relaxed NP-hard problem. The relaxations we consider decompose the original problem into two non-overlapping parts: an easy LP-tight part and a difficult one. For the latter part a combinatorial solver must be used. As we show in our experiments, in a number of applications the second, difficult part constitutes only a small fraction of the whole problem. This property allows to significantly reduce the computational time of the combinatorial solver and therefore solve problems which were out of reach before.

Discrete graphical models -- an optimization perspective

This monograph is about discrete energy minimization for discrete graphical models. It considers graphical models, or, more precisely, maximum a posteriori inference for graphical models, purely as a combinatorial optimization problem. Modeling, applications, probabilistic interpretations and many other aspects are either ignored here or find their place in examples and remarks only. It covers the integer linear programming formulation of the problem as well as its linear programming, Lagrange and Lagrange decomposition-based relaxations. In particular, it provides a detailed analysis of the polynomially solvable acyclic and submodular problems, along with the corresponding exact optimization methods. Major approximate methods, such as message passing and graph cut techniques are also described and analyzed comprehensively. The monograph can be useful for undergraduate and graduate students studying optimization or graphical models, as well as for experts in optimization who want to have a look into graphical models. To make the monograph suitable for both categories of readers we explicitly separate the mathematical optimization background chapters from those specific to graphical models.