A Primal-Dual Solver for Large-Scale Tracking-by-Assignment
Paper and Code
Apr 14, 2020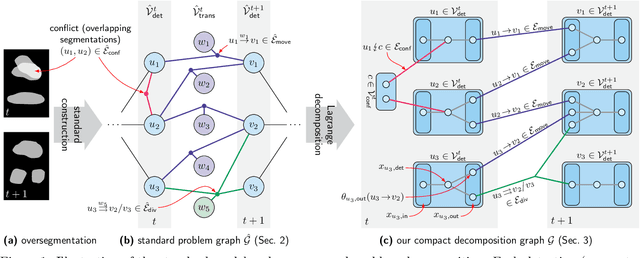
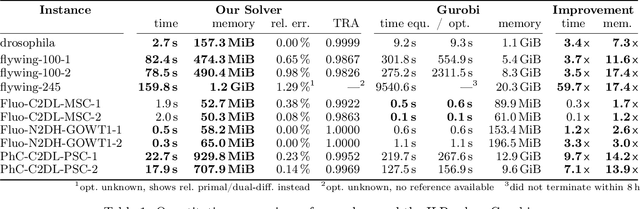
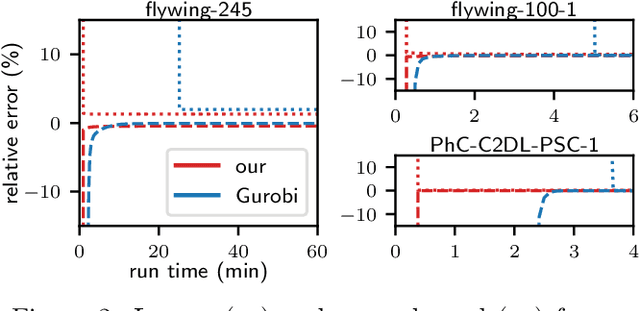
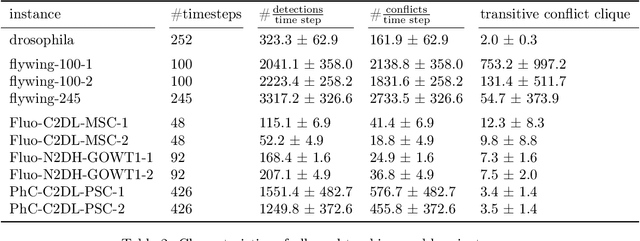
We propose a fast approximate solver for the combinatorial problem known as tracking-by-assignment, which we apply to cell tracking. The latter plays a key role in discovery in many life sciences, especially in cell and developmental biology. So far, in the most general setting this problem was addressed by off-the-shelf solvers like Gurobi, whose run time and memory requirements rapidly grow with the size of the input. In contrast, for our method this growth is nearly linear. Our contribution consists of a new (1) decomposable compact representation of the problem; (2) dual block-coordinate ascent method for optimizing the decomposition-based dual; and (3) primal heuristics that reconstructs a feasible integer solution based on the dual information. Compared to solving the problem with Gurobi, we observe an up to~60~times speed-up, while reducing the memory footprint significantly. We demonstrate the efficacy of our method on real-world tracking problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge