Fully Unsupervised Annotation of C. Elegans

In this work we present a novel approach for unsupervised multi-graph matching, which applies to problems for which a Gaussian distribution of keypoint features can be assumed. We leverage cycle consistency as loss for self-supervised learning, and determine Gaussian parameters through Bayesian Optimization, yielding a highly efficient approach that scales to large datasets. Our fully unsupervised approach enables us to reach the accuracy of state-of-the-art supervised methodology for the use case of annotating cell nuclei in 3D microscopy images of the worm C. elegans. To this end, our approach yields the first unsupervised atlas of C. elegans, i.e. a model of the joint distribution of all of its cell nuclei, without the need for any ground truth cell annotation. This advancement enables highly efficient annotation of cell nuclei in large microscopy datasets of C. elegans. Beyond C. elegans, our approach offers fully unsupervised construction of cell-level atlases for any model organism with a stereotyped cell lineage, and thus bears the potential to catalyze respective comparative developmental studies in a range of further species.

Unlocking the Potential of Operations Research for Multi-Graph Matching

We consider the incomplete multi-graph matching problem, which is a generalization of the NP-hard quadratic assignment problem for matching multiple finite sets. Multi-graph matching plays a central role in computer vision, e.g., for matching images or shapes, so that a number of dedicated optimization techniques have been proposed. While the closely related NP-hard multi-dimensional assignment problem (MDAP) has been studied for decades in the operations research community, it only considers complete matchings and has a different cost structure. We bridge this gap and transfer well-known approximation algorithms for the MDAP to incomplete multi-graph matching. To this end, we revisit respective algorithms, adapt them to incomplete multi-graph matching, and propose their extended and parallelized versions. Our experimental validation shows that our new method substantially outperforms the previous state of the art in terms of objective and runtime. Our algorithm matches, for example, 29 images with more than 500 keypoints each in less than two minutes, whereas the fastest considered competitor requires at least half an hour while producing far worse results.

A Comparative Study of Graph Matching Algorithms in Computer Vision

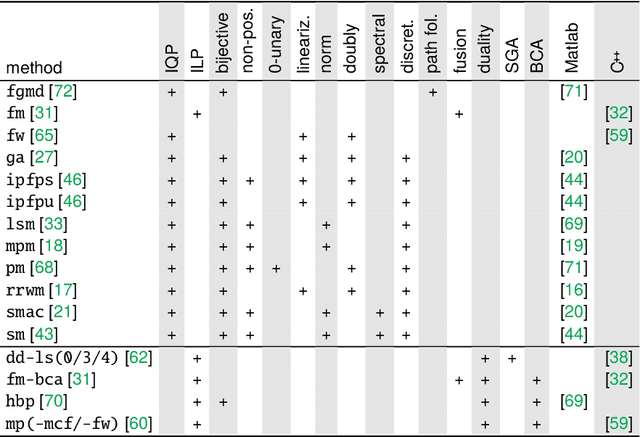
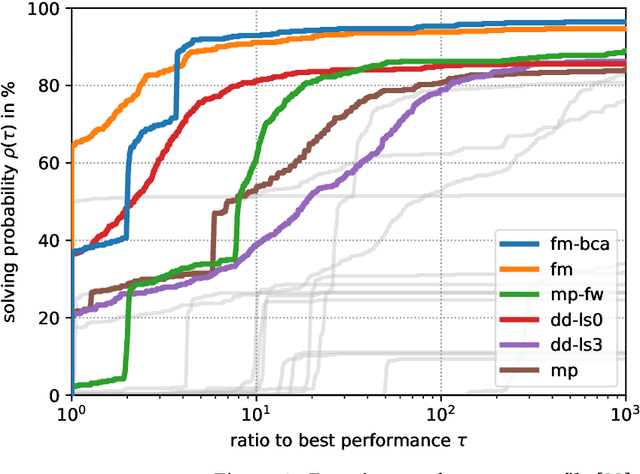
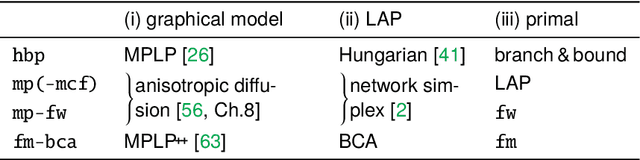
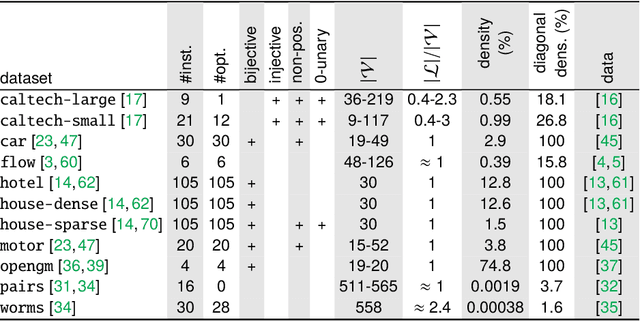
The graph matching optimization problem is an essential component for many tasks in computer vision, such as bringing two deformable objects in correspondence. Naturally, a wide range of applicable algorithms have been proposed in the last decades. Since a common standard benchmark has not been developed, their performance claims are often hard to verify as evaluation on differing problem instances and criteria make the results incomparable. To address these shortcomings, we present a comparative study of graph matching algorithms. We create a uniform benchmark where we collect and categorize a large set of existing and publicly available computer vision graph matching problems in a common format. At the same time we collect and categorize the most popular open-source implementations of graph matching algorithms. Their performance is evaluated in a way that is in line with the best practices for comparing optimization algorithms. The study is designed to be reproducible and extensible to serve as a valuable resource in the future. Our study provides three notable insights: 1.) popular problem instances are exactly solvable in substantially less than 1 second and, therefore, are insufficient for future empirical evaluations; 2.) the most popular baseline methods are highly inferior to the best available methods; 3.) despite the NP-hardness of the problem, instances coming from vision applications are often solvable in a few seconds even for graphs with more than 500 vertices.

Fusion Moves for Graph Matching

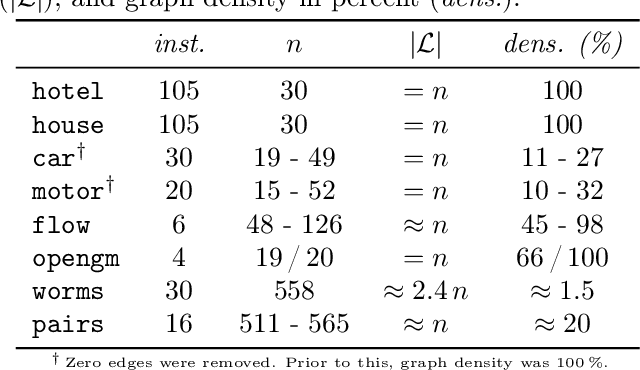
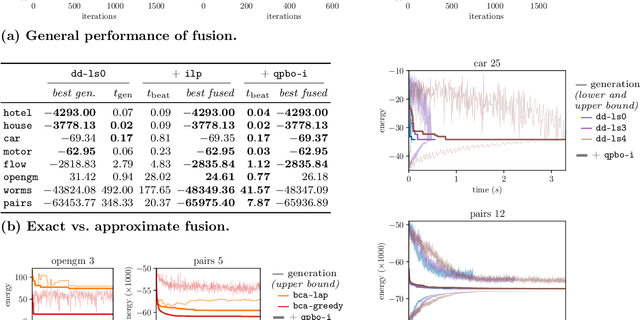
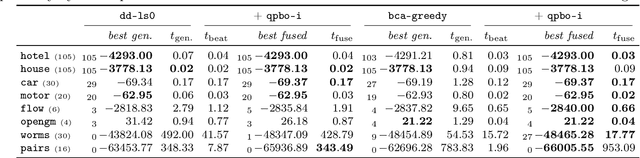
We contribute to approximate algorithms for the quadratic assignment problem also known as graph matching. Inspired by the success of the fusion moves technique developed for multilabel discrete Markov random fields, we investigate its applicability to graph matching. In particular, we show how it can be efficiently combined with the dedicated state-of-the-art Lagrange dual methods that have recently shown superior results in computer vision and bio-imaging applications. As our empirical evaluation on a wide variety of graph matching datasets suggests, fusion moves notably improve performance of these methods in terms of speed and quality of the obtained solutions. Hence, this combination results in a state-of-the-art solver for graph matching.

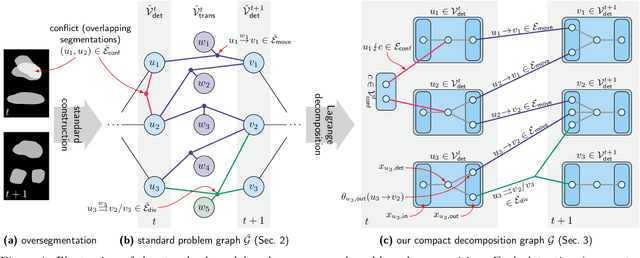
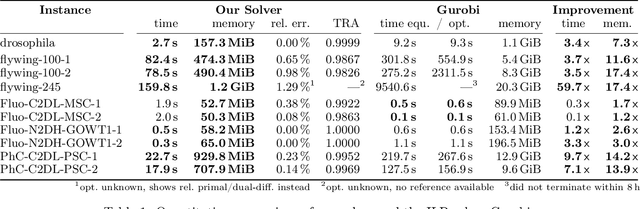
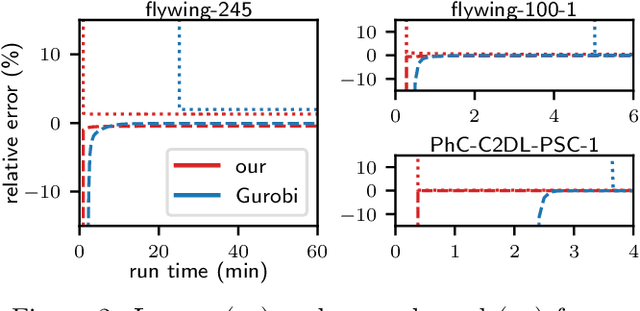
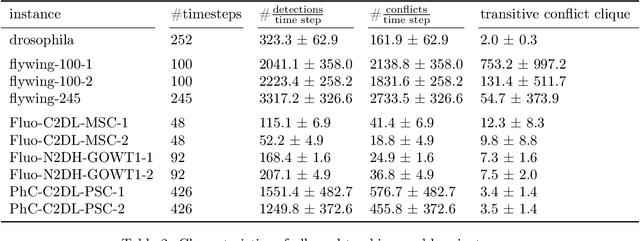
A Primal-Dual Solver for Large-Scale Tracking-by-Assignment

We propose a fast approximate solver for the combinatorial problem known as tracking-by-assignment, which we apply to cell tracking. The latter plays a key role in discovery in many life sciences, especially in cell and developmental biology. So far, in the most general setting this problem was addressed by off-the-shelf solvers like Gurobi, whose run time and memory requirements rapidly grow with the size of the input. In contrast, for our method this growth is nearly linear. Our contribution consists of a new (1) decomposable compact representation of the problem; (2) dual block-coordinate ascent method for optimizing the decomposition-based dual; and (3) primal heuristics that reconstructs a feasible integer solution based on the dual information. Compared to solving the problem with Gurobi, we observe an up to~60~times speed-up, while reducing the memory footprint significantly. We demonstrate the efficacy of our method on real-world tracking problems.