Lorenz Feineis
A Comparative Study of Graph Matching Algorithms in Computer Vision
Jul 01, 2022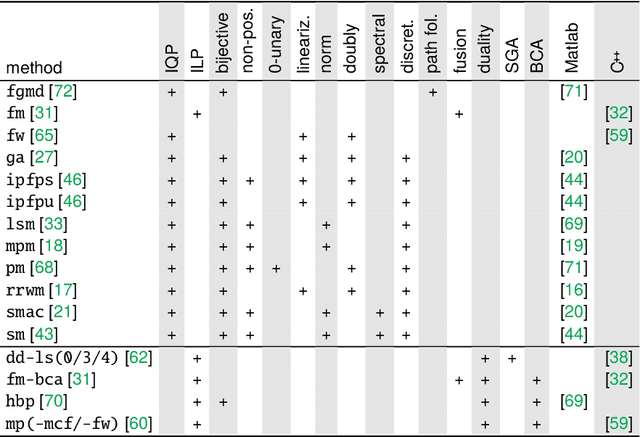
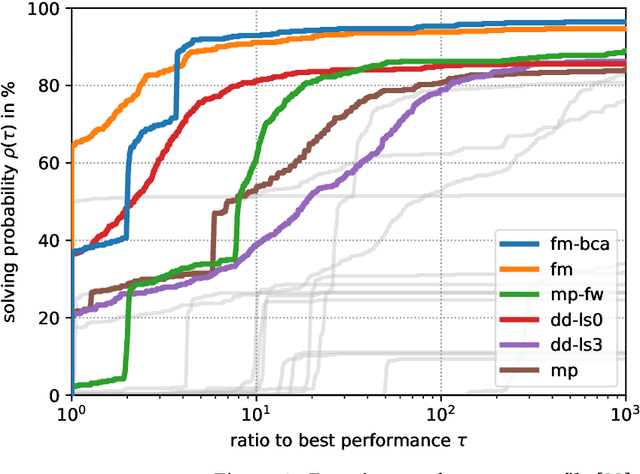
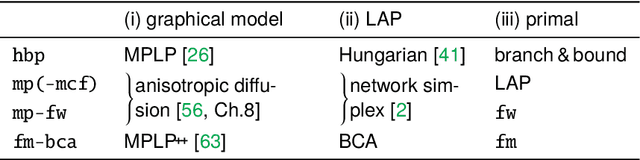
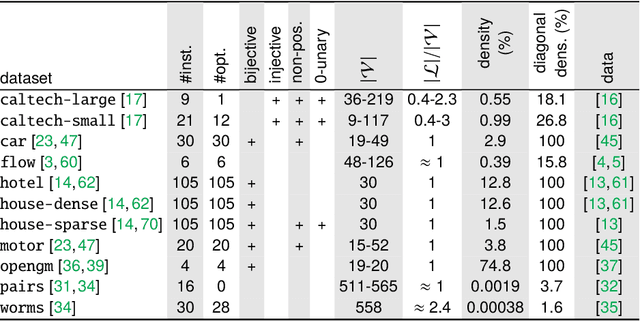
Abstract:The graph matching optimization problem is an essential component for many tasks in computer vision, such as bringing two deformable objects in correspondence. Naturally, a wide range of applicable algorithms have been proposed in the last decades. Since a common standard benchmark has not been developed, their performance claims are often hard to verify as evaluation on differing problem instances and criteria make the results incomparable. To address these shortcomings, we present a comparative study of graph matching algorithms. We create a uniform benchmark where we collect and categorize a large set of existing and publicly available computer vision graph matching problems in a common format. At the same time we collect and categorize the most popular open-source implementations of graph matching algorithms. Their performance is evaluated in a way that is in line with the best practices for comparing optimization algorithms. The study is designed to be reproducible and extensible to serve as a valuable resource in the future. Our study provides three notable insights: 1.) popular problem instances are exactly solvable in substantially less than 1 second and, therefore, are insufficient for future empirical evaluations; 2.) the most popular baseline methods are highly inferior to the best available methods; 3.) despite the NP-hardness of the problem, instances coming from vision applications are often solvable in a few seconds even for graphs with more than 500 vertices.
Fusion Moves for Graph Matching
Feb 05, 2021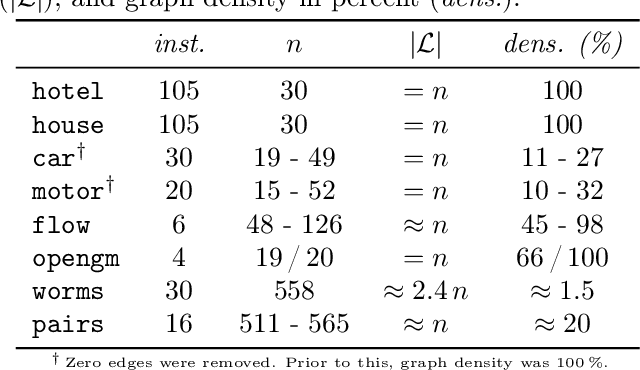
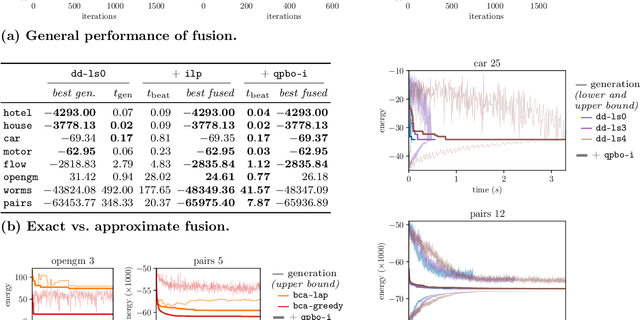
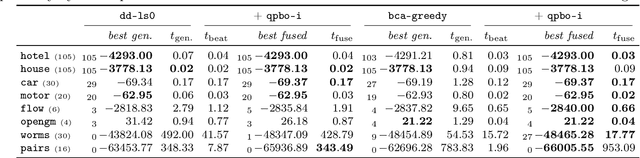

Abstract:We contribute to approximate algorithms for the quadratic assignment problem also known as graph matching. Inspired by the success of the fusion moves technique developed for multilabel discrete Markov random fields, we investigate its applicability to graph matching. In particular, we show how it can be efficiently combined with the dedicated state-of-the-art Lagrange dual methods that have recently shown superior results in computer vision and bio-imaging applications. As our empirical evaluation on a wide variety of graph matching datasets suggests, fusion moves notably improve performance of these methods in terms of speed and quality of the obtained solutions. Hence, this combination results in a state-of-the-art solver for graph matching.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge