Tobias Pietzsch
A Primal-Dual Solver for Large-Scale Tracking-by-Assignment
Apr 14, 2020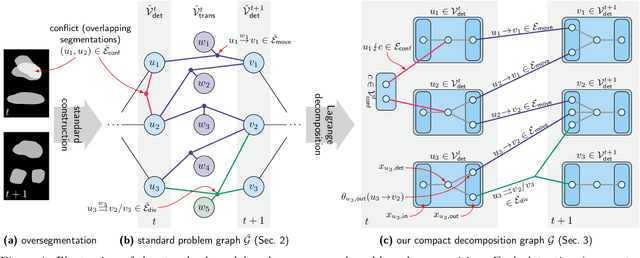
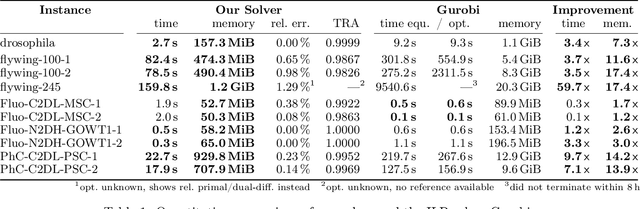
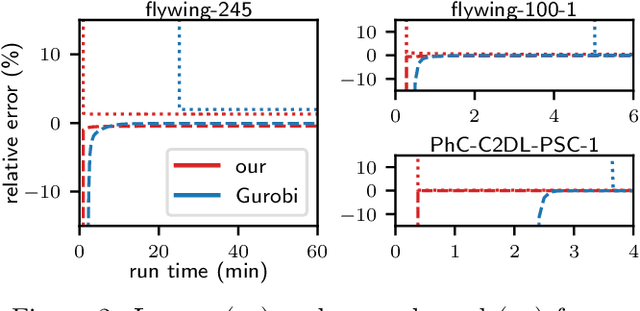
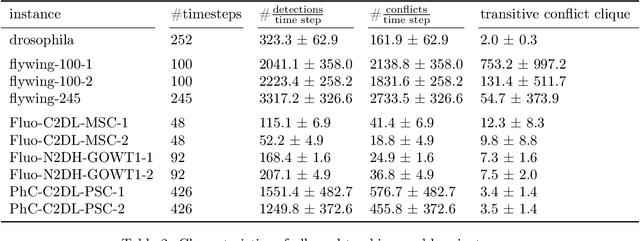
Abstract:We propose a fast approximate solver for the combinatorial problem known as tracking-by-assignment, which we apply to cell tracking. The latter plays a key role in discovery in many life sciences, especially in cell and developmental biology. So far, in the most general setting this problem was addressed by off-the-shelf solvers like Gurobi, whose run time and memory requirements rapidly grow with the size of the input. In contrast, for our method this growth is nearly linear. Our contribution consists of a new (1) decomposable compact representation of the problem; (2) dual block-coordinate ascent method for optimizing the decomposition-based dual; and (3) primal heuristics that reconstructs a feasible integer solution based on the dual information. Compared to solving the problem with Gurobi, we observe an up to~60~times speed-up, while reducing the memory footprint significantly. We demonstrate the efficacy of our method on real-world tracking problems.
The Candidate Multi-Cut for Cell Segmentation
Jul 04, 2017
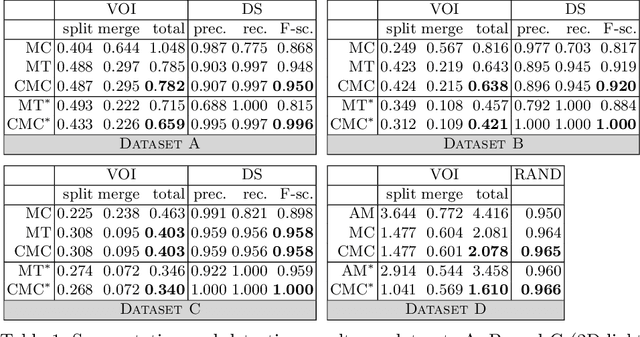


Abstract:Two successful approaches for the segmentation of biomedical images are (1) the selection of segment candidates from a merge-tree, and (2) the clustering of small superpixels by solving a Multi-Cut problem. In this paper, we introduce a model that unifies both approaches. Our model, the Candidate Multi-Cut (CMC), allows joint selection and clustering of segment candidates from a merge-tree. This way, we overcome the respective limitations of the individual methods: (1) the space of possible segmentations is not constrained to candidates of a merge-tree, and (2) the decision for clustering can be made on candidates larger than superpixels, using features over larger contexts. We solve the optimization problem of selecting and clustering of candidates using an integer linear program. On datasets of 2D light microscopy of cell populations and 3D electron microscopy of neurons, we show that our method generalizes well and generates more accurate segmentations than merge-tree or Multi-Cut methods alone.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge