Taxonomy of Dual Block-Coordinate Ascent Methods for Discrete Energy Minimization
Paper and Code
Apr 16, 2020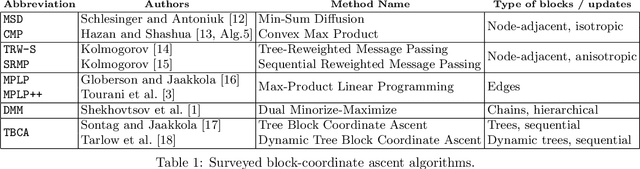
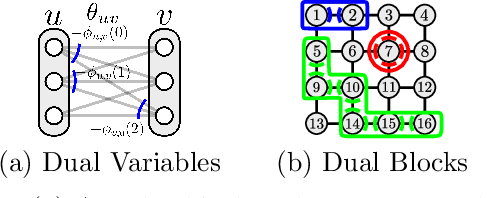
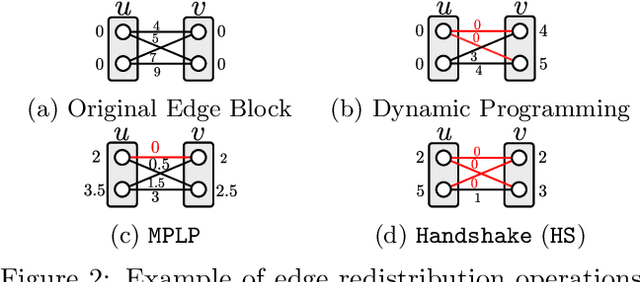
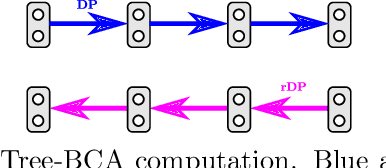
We consider the maximum-a-posteriori inference problem in discrete graphical models and study solvers based on the dual block-coordinate ascent rule. We map all existing solvers in a single framework, allowing for a better understanding of their design principles. We theoretically show that some block-optimizing updates are sub-optimal and how to strictly improve them. On a wide range of problem instances of varying graph connectivity, we study the performance of existing solvers as well as new variants that can be obtained within the framework. As a result of this exploration we build a new state-of-the art solver, performing uniformly better on the whole range of test instances.
* Accepted in AISTATS 2020
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge