Deep Multivariate Models with Parametric Conditionals

We consider deep multivariate models for heterogeneous collections of random variables. In the context of computer vision, such collections may e.g. consist of images, segmentations, image attributes, and latent variables. When developing such models, most existing works start from an application task and design the model components and their dependencies to meet the needs of the chosen task. This has the disadvantage of limiting the applicability of the resulting model for other downstream tasks. Here, instead, we propose to represent the joint probability distribution by means of conditional probability distributions for each group of variables conditioned on the rest. Such models can then be used for practically any possible downstream task. Their learning can be approached as training a parametrised Markov chain kernel by maximising the data likelihood of its limiting distribution. This has the additional advantage of allowing a wide range of semi-supervised learning scenarios.

Symmetric Equilibrium Learning of VAEs

We view variational autoencoders (VAE) as decoder-encoder pairs, which map distributions in the data space to distributions in the latent space and vice versa. The standard learning approach for VAEs, i.e. maximisation of the evidence lower bound (ELBO), has an obvious asymmetry in that respect. Moreover, it requires a closed form a-priori latent distribution. This limits the applicability of VAEs in more complex scenarios, such as general semi-supervised learning and employing complex generative models as priors. We propose a Nash equilibrium learning approach that relaxes these restrictions and allows learning VAEs in situations where both the data and the latent distributions are accessible only by sampling. The flexibility and simplicity of this approach allows its application to a wide range of learning scenarios and downstream tasks. We show experimentally that the models learned by this method are comparable to those obtained by ELBO learning and demonstrate its applicability for tasks that are not accessible by standard VAE learning.

Bias-Variance Tradeoffs in Single-Sample Binary Gradient Estimators

Discrete and especially binary random variables occur in many machine learning models, notably in variational autoencoders with binary latent states and in stochastic binary networks. When learning such models, a key tool is an estimator of the gradient of the expected loss with respect to the probabilities of binary variables. The straight-through (ST) estimator gained popularity due to its simplicity and efficiency, in particular in deep networks where unbiased estimators are impractical. Several techniques were proposed to improve over ST while keeping the same low computational complexity: Gumbel-Softmax, ST-Gumbel-Softmax, BayesBiNN, FouST. We conduct a theoretical analysis of bias and variance of these methods in order to understand tradeoffs and verify the originally claimed properties. The presented theoretical results allow for better understanding of these methods and in some cases reveal serious issues.

VAE Approximation Error: ELBO and Conditional Independence

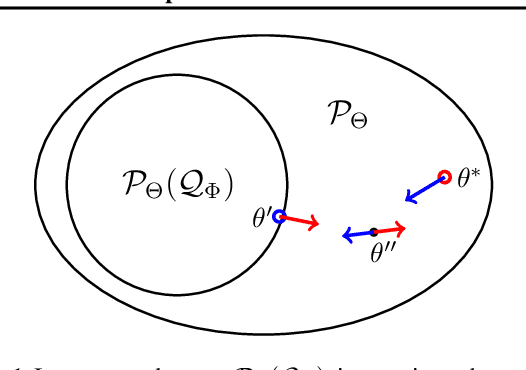
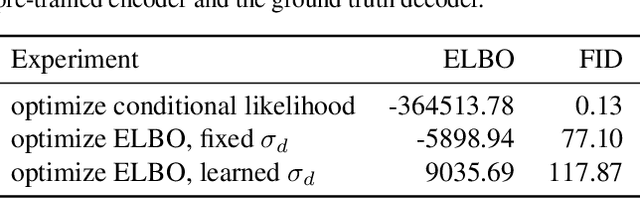
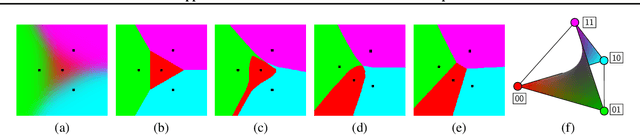
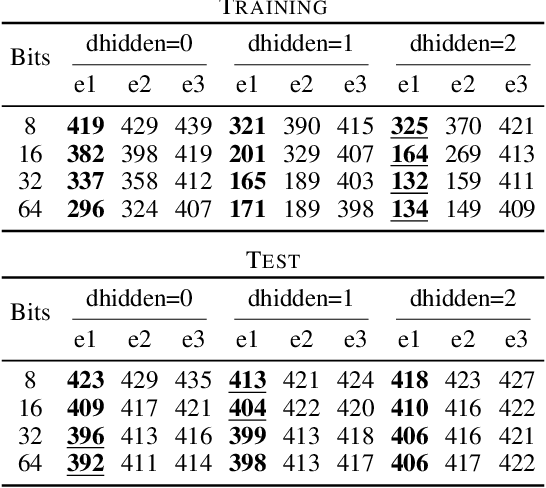
The importance of Variational Autoencoders reaches far beyond standalone generative models -- the approach is also used for learning latent representations and can be generalized to semi-supervised learning. This requires a thorough analysis of their commonly known shortcomings: posterior collapse and approximation errors. This paper analyzes VAE approximation errors caused by the combination of the ELBO objective with the choice of the encoder probability family, in particular under conditional independence assumptions. We identify the subclass of generative models consistent with the encoder family. We show that the ELBO optimizer is pulled from the likelihood optimizer towards this consistent subset. Furthermore, this subset can not be enlarged, and the respective error cannot be decreased, by only considering deeper encoder networks.

Reintroducing Straight-Through Estimators as Principled Methods for Stochastic Binary Networks

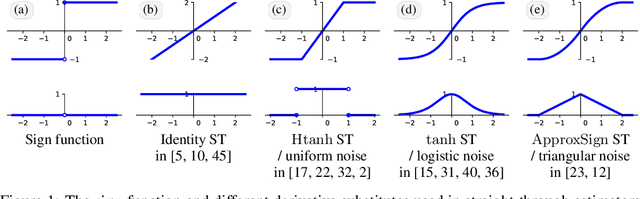
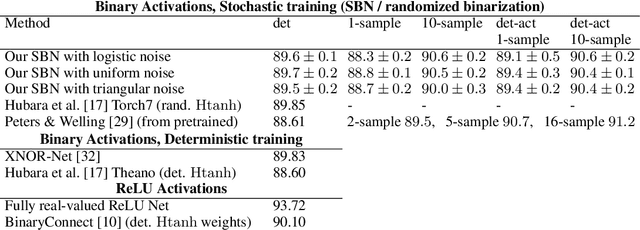
Training neural networks with binary weights and activations is a challenging problem due to the lack of gradients and difficulty of optimization over discrete weights. Many successful experimental results have been recently achieved using the empirical straight-through estimation approach. This approach has generated a variety of ad-hoc rules for propagating gradients through non-differentiable activations and updating discrete weights. We put such methods on a solid basis by obtaining them as viable approximations in the stochastic binary network (SBN) model with Bernoulli weights. In this model gradients are well-defined and the weight probabilities can be optimized by continuous techniques. By choosing the activation noises in SBN appropriately and choosing mirror descent (MD) for optimization, we obtain methods that closely resemble several existing straight-through variants, but unlike them, all work reliably and produce equally good results. We further show that variational inference for Bayesian learning of Binary weights can be implemented using MD updates with the same simplicity.

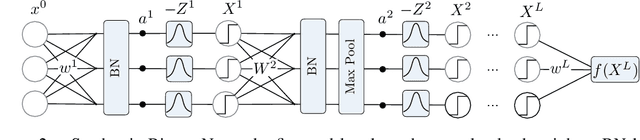
Path Sample-Analytic Gradient Estimators for Stochastic Binary Networks

In networks with binary activations and or binary weights the training by gradient descent is complicated as the model has piecewise constant response. We consider stochastic binary networks, obtained by adding noises in front of activations. The expected model response becomes a smooth function of parameters, its gradient is well defined but is challenging to estimate accurately. We propose a new method for this estimation problem combining sampling and analytic approximation steps. The method has a significantly reduced variance at the price of a small bias which gives a very practical tradeoff in comparison with existing unbiased and biased estimators. We further show that one extra linearization step leads to a deep straight-through estimator previously known only as an ad-hoc heuristic. We experimentally show higher accuracy in gradient estimation and demonstrate a more stable and better performing training in deep convolutional models with both proposed methods.

MPLP++: Fast, Parallel Dual Block-Coordinate Ascent for Dense Graphical Models

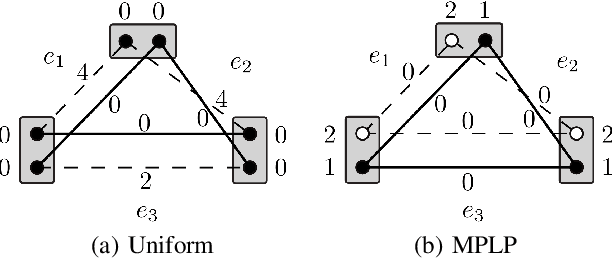
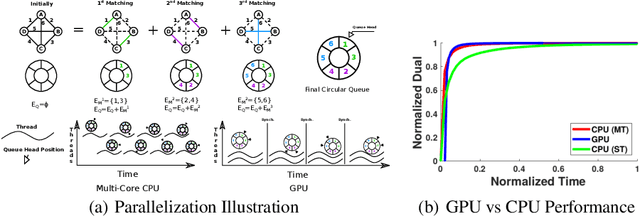
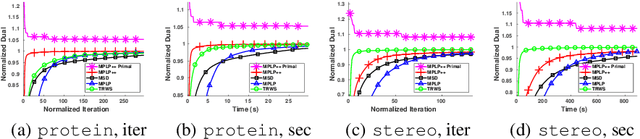
Dense, discrete Graphical Models with pairwise potentials are a powerful class of models which are employed in state-of-the-art computer vision and bio-imaging applications. This work introduces a new MAP-solver, based on the popular Dual Block-Coordinate Ascent principle. Surprisingly, by making a small change to the low-performing solver, the Max Product Linear Programming (MPLP) algorithm, we derive the new solver MPLP++ that significantly outperforms all existing solvers by a large margin, including the state-of-the-art solver Tree-Reweighted Sequential (TRWS) message-passing algorithm. Additionally, our solver is highly parallel, in contrast to TRWS, which gives a further boost in performance with the proposed GPU and multi-thread CPU implementations. We verify the superiority of our algorithm on dense problems from publicly available benchmarks, as well, as a new benchmark for 6D Object Pose estimation. We also provide an ablation study with respect to graph density.

Taxonomy of Dual Block-Coordinate Ascent Methods for Discrete Energy Minimization

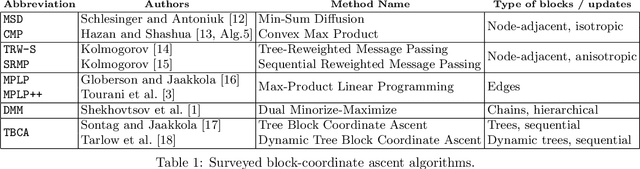
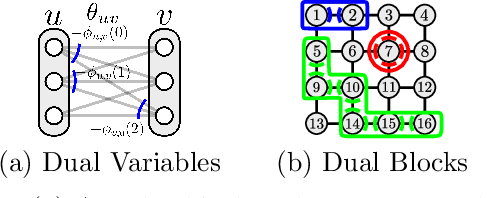
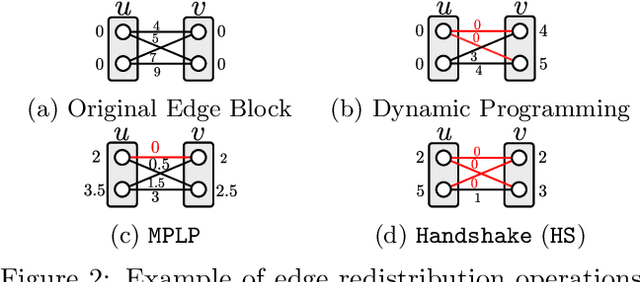
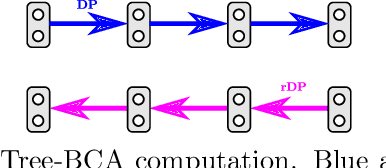
We consider the maximum-a-posteriori inference problem in discrete graphical models and study solvers based on the dual block-coordinate ascent rule. We map all existing solvers in a single framework, allowing for a better understanding of their design principles. We theoretically show that some block-optimizing updates are sub-optimal and how to strictly improve them. On a wide range of problem instances of varying graph connectivity, we study the performance of existing solvers as well as new variants that can be obtained within the framework. As a result of this exploration we build a new state-of-the art solver, performing uniformly better on the whole range of test instances.

Belief Propagation Reloaded: Learning BP-Layers for Labeling Problems

It has been proposed by many researchers that combining deep neural networks with graphical models can create more efficient and better regularized composite models. The main difficulties in implementing this in practice are associated with a discrepancy in suitable learning objectives as well as with the necessity of approximations for the inference. In this work we take one of the simplest inference methods, a truncated max-product Belief Propagation, and add what is necessary to make it a proper component of a deep learning model: We connect it to learning formulations with losses on marginals and compute the backprop operation. This BP-Layer can be used as the final or an intermediate block in convolutional neural networks (CNNs), allowing us to design a hierarchical model composing BP inference and CNNs at different scale levels. The model is applicable to a range of dense prediction problems, is well-trainable and provides parameter-efficient and robust solutions in stereo, optical flow and semantic segmentation.

Stochastic Normalizations as Bayesian Learning

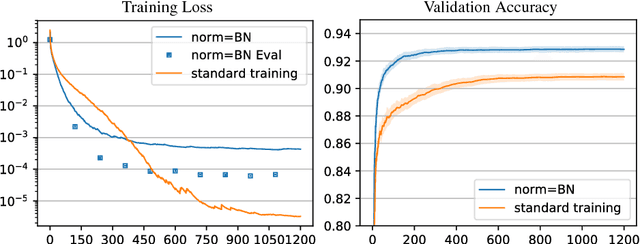
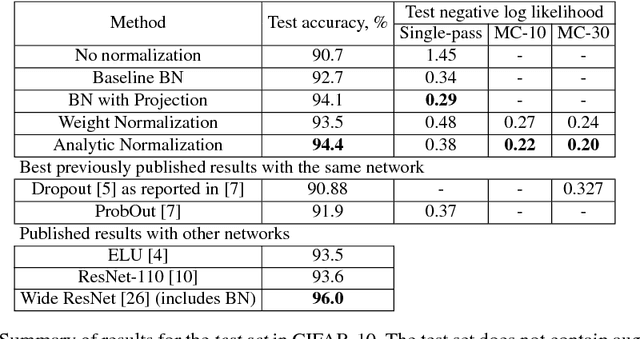
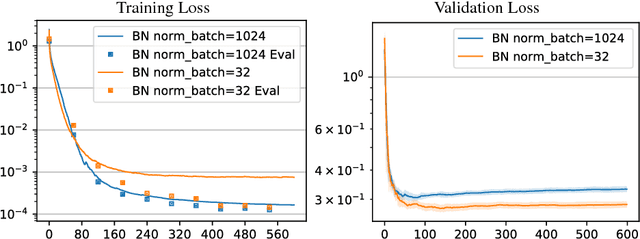
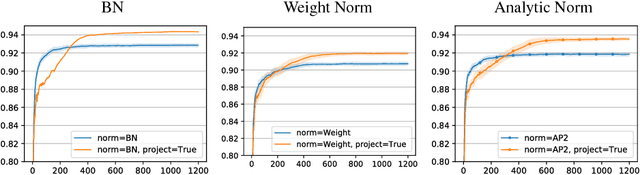
In this work we investigate the reasons why Batch Normalization (BN) improves the generalization performance of deep networks. We argue that one major reason, distinguishing it from data-independent normalization methods, is randomness of batch statistics. This randomness appears in the parameters rather than in activations and admits an interpretation as a practical Bayesian learning. We apply this idea to other (deterministic) normalization techniques that are oblivious to the batch size. We show that their generalization performance can be improved significantly by Bayesian learning of the same form. We obtain test performance comparable to BN and, at the same time, better validation losses suitable for subsequent output uncertainty estimation through approximate Bayesian posterior.