Stochastic Normalizations as Bayesian Learning
Paper and Code
Nov 01, 2018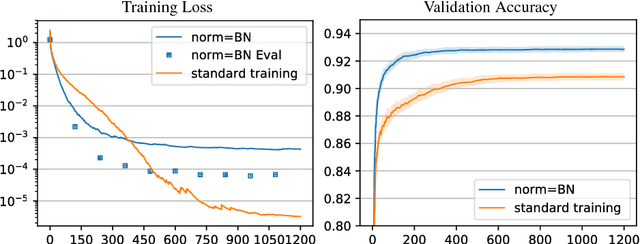
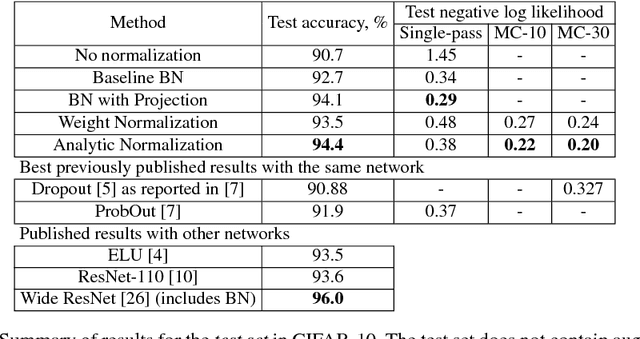
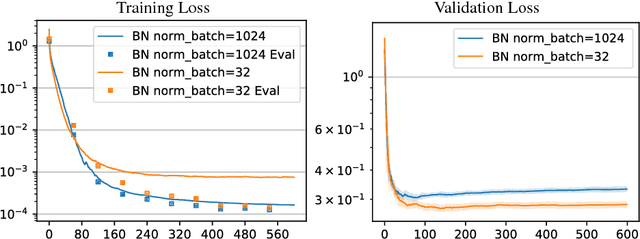
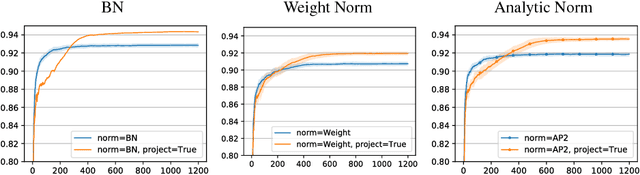
In this work we investigate the reasons why Batch Normalization (BN) improves the generalization performance of deep networks. We argue that one major reason, distinguishing it from data-independent normalization methods, is randomness of batch statistics. This randomness appears in the parameters rather than in activations and admits an interpretation as a practical Bayesian learning. We apply this idea to other (deterministic) normalization techniques that are oblivious to the batch size. We show that their generalization performance can be improved significantly by Bayesian learning of the same form. We obtain test performance comparable to BN and, at the same time, better validation losses suitable for subsequent output uncertainty estimation through approximate Bayesian posterior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge