Symmetric Equilibrium Learning of VAEs

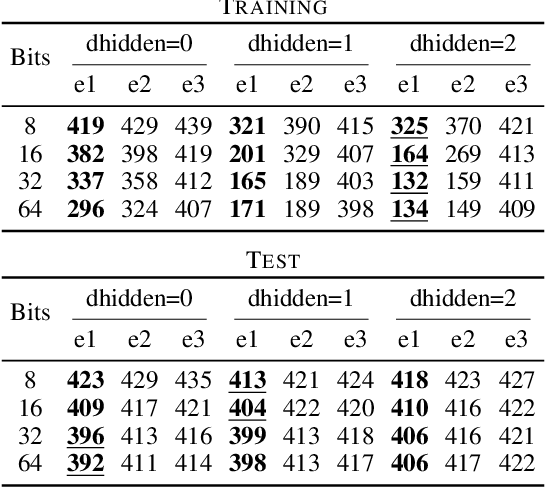
We view variational autoencoders (VAE) as decoder-encoder pairs, which map distributions in the data space to distributions in the latent space and vice versa. The standard learning approach for VAEs, i.e. maximisation of the evidence lower bound (ELBO), has an obvious asymmetry in that respect. Moreover, it requires a closed form a-priori latent distribution. This limits the applicability of VAEs in more complex scenarios, such as general semi-supervised learning and employing complex generative models as priors. We propose a Nash equilibrium learning approach that relaxes these restrictions and allows learning VAEs in situations where both the data and the latent distributions are accessible only by sampling. The flexibility and simplicity of this approach allows its application to a wide range of learning scenarios and downstream tasks. We show experimentally that the models learned by this method are comparable to those obtained by ELBO learning and demonstrate its applicability for tasks that are not accessible by standard VAE learning.

VAE Approximation Error: ELBO and Conditional Independence

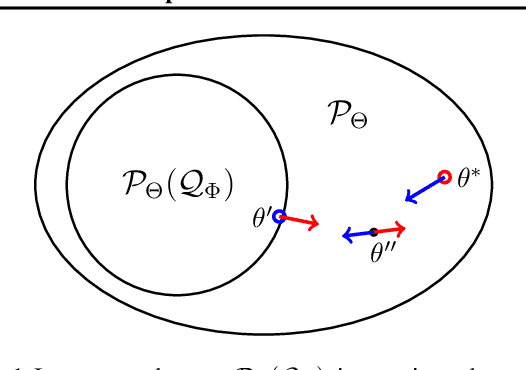
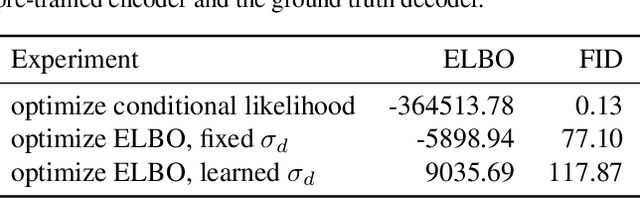
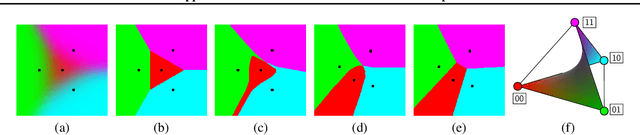
The importance of Variational Autoencoders reaches far beyond standalone generative models -- the approach is also used for learning latent representations and can be generalized to semi-supervised learning. This requires a thorough analysis of their commonly known shortcomings: posterior collapse and approximation errors. This paper analyzes VAE approximation errors caused by the combination of the ELBO objective with the choice of the encoder probability family, in particular under conditional independence assumptions. We identify the subclass of generative models consistent with the encoder family. We show that the ELBO optimizer is pulled from the likelihood optimizer towards this consistent subset. Furthermore, this subset can not be enlarged, and the respective error cannot be decreased, by only considering deeper encoder networks.

Path Sample-Analytic Gradient Estimators for Stochastic Binary Networks

In networks with binary activations and or binary weights the training by gradient descent is complicated as the model has piecewise constant response. We consider stochastic binary networks, obtained by adding noises in front of activations. The expected model response becomes a smooth function of parameters, its gradient is well defined but is challenging to estimate accurately. We propose a new method for this estimation problem combining sampling and analytic approximation steps. The method has a significantly reduced variance at the price of a small bias which gives a very practical tradeoff in comparison with existing unbiased and biased estimators. We further show that one extra linearization step leads to a deep straight-through estimator previously known only as an ad-hoc heuristic. We experimentally show higher accuracy in gradient estimation and demonstrate a more stable and better performing training in deep convolutional models with both proposed methods.

Stochastic Normalizations as Bayesian Learning

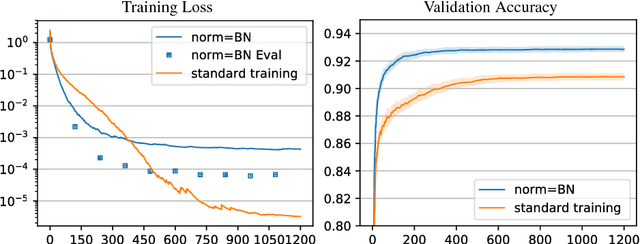
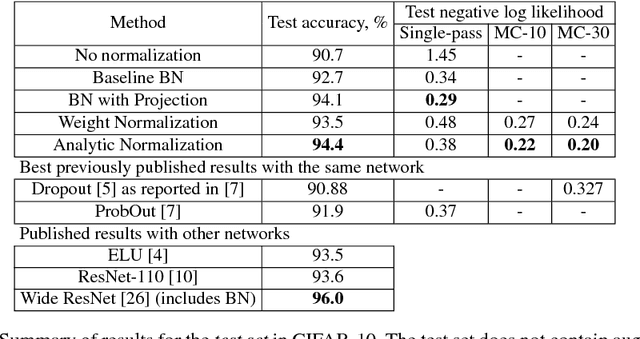
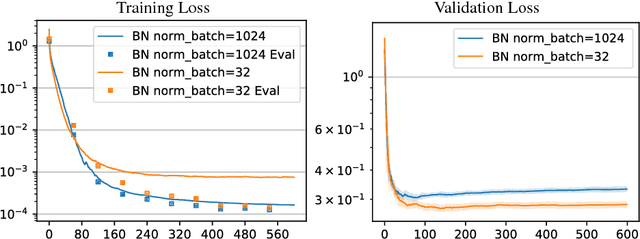
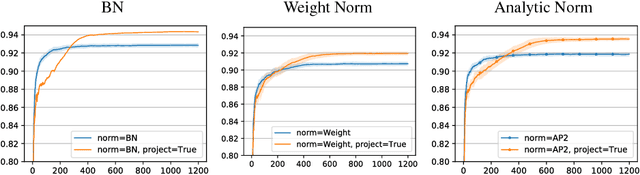
In this work we investigate the reasons why Batch Normalization (BN) improves the generalization performance of deep networks. We argue that one major reason, distinguishing it from data-independent normalization methods, is randomness of batch statistics. This randomness appears in the parameters rather than in activations and admits an interpretation as a practical Bayesian learning. We apply this idea to other (deterministic) normalization techniques that are oblivious to the batch size. We show that their generalization performance can be improved significantly by Bayesian learning of the same form. We obtain test performance comparable to BN and, at the same time, better validation losses suitable for subsequent output uncertainty estimation through approximate Bayesian posterior.

Feed-forward Uncertainty Propagation in Belief and Neural Networks

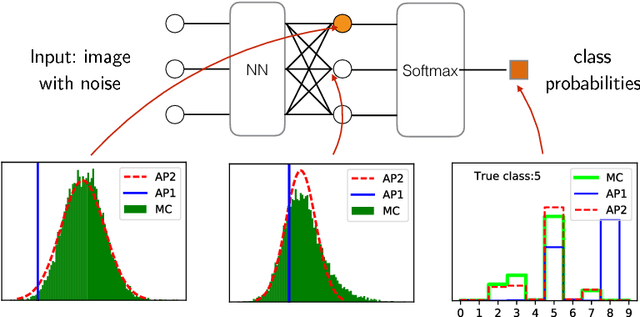
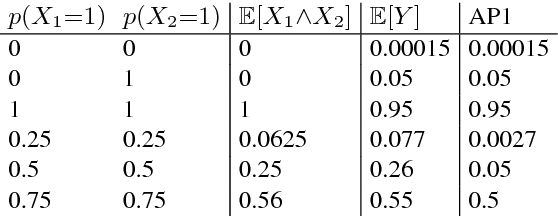
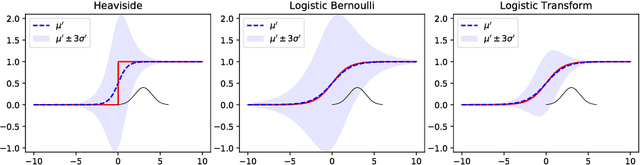
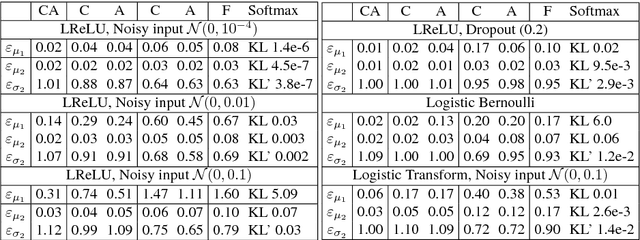
We propose a feed-forward inference method applicable to belief and neural networks. In a belief network, the method estimates an approximate factorized posterior of all hidden units given the input. In neural networks the method propagates uncertainty of the input through all the layers. In neural networks with injected noise, the method analytically takes into account uncertainties resulting from this noise. Such feed-forward analytic propagation is differentiable in parameters and can be trained end-to-end. Compared to standard NN, which can be viewed as propagating only the means, we propagate the mean and variance. The method can be useful in all scenarios that require knowledge of the neuron statistics, e.g. when dealing with uncertain inputs, considering sigmoid activations as probabilities of Bernoulli units, training the models regularized by injected noise (dropout) or estimating activation statistics over the dataset (as needed for normalization methods). In the experiments we show the possible utility of the method in all these tasks as well as its current limitations.

Normalization of Neural Networks using Analytic Variance Propagation

We address the problem of estimating statistics of hidden units in a neural network using a method of analytic moment propagation. These statistics are useful for approximate whitening of the inputs in front of saturating non-linearities such as a sigmoid function. This is important for initialization of training and for reducing the accumulated scale and bias dependencies (compensating covariate shift), which presumably eases the learning. In batch normalization, which is currently a very widely applied technique, sample estimates of statistics of hidden units over a batch are used. The proposed estimation uses an analytic propagation of mean and variance of the training set through the network. The result depends on the network structure and its current weights but not on the specific batch input. The estimates are suitable for initialization and normalization, efficient to compute and independent of the batch size. The experimental verification well supports these claims. However, the method does not share the generalization properties of BN, to which our experiments give some additional insight.

Generative learning for deep networks

Learning, taking into account full distribution of the data, referred to as generative, is not feasible with deep neural networks (DNNs) because they model only the conditional distribution of the outputs given the inputs. Current solutions are either based on joint probability models facing difficult estimation problems or learn two separate networks, mapping inputs to outputs (recognition) and vice-versa (generation). We propose an intermediate approach. First, we show that forward computation in DNNs with logistic sigmoid activations corresponds to a simplified approximate Bayesian inference in a directed probabilistic multi-layer model. This connection allows to interpret DNN as a probabilistic model of the output and all hidden units given the input. Second, we propose that in order for the recognition and generation networks to be more consistent with the joint model of the data, weights of the recognition and generator network should be related by transposition. We demonstrate in a tentative experiment that such a coupled pair can be learned generatively, modelling the full distribution of the data, and has enough capacity to perform well in both recognition and generation.

M-best solutions for a class of fuzzy constraint satisfaction problems

The article considers one of the possible generalizations of constraint satisfaction problems where relations are replaced by multivalued membership functions. In this case operations of disjunction and conjunction are replaced by maximum and minimum, and consistency of a solution becomes multivalued rather than binary. The article studies the problem of finding d most admissible solutions for a given d. A tractable subclass of these problems is defined by the concepts of invariants and polymorphisms similar to the classic constraint satisfaction approach. These concepts are adapted in two ways. Firstly, the correspondence of "invariant-polymorphism" is generalized to (min,max) semirings. Secondly, we consider non-uniform polymorphisms, where each variable has its own operator, in contrast to the case of one operator common for all variables. The article describes an algorithm that finds $d$ most admissible solutions in polynomial time, provided that the problem is invariant with respect to some non-uniform majority operator. It is essential that this operator needs not to be known for the algorithm to work. Moreover, even a guarantee for the existence of such an operator is not necessary. The algorithm either finds the solution or discards the problem. The latter is possible only if the problem has no majority polymorphism.

A class of random fields on complete graphs with tractable partition function

The aim of this short note is to draw attention to a method by which the partition function and marginal probabilities for a certain class of random fields on complete graphs can be computed in polynomial time. This class includes Ising models with homogeneous pairwise potentials but arbitrary (inhomogeneous) unary potentials. Similarly, the partition function and marginal probabilities can be computed in polynomial time for random fields on complete bipartite graphs, provided they have homogeneous pairwise potentials. We expect that these tractable classes of large scale random fields can be very useful for the evaluation of approximation algorithms by providing exact error estimates.

Modelling Distributed Shape Priors by Gibbs Random Fields of Second Order

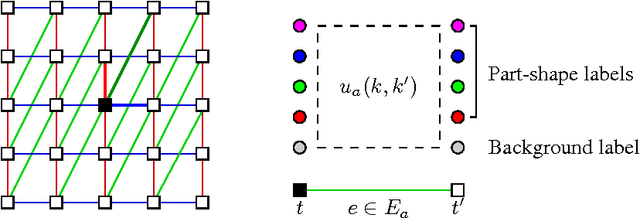
We analyse the potential of Gibbs Random Fields for shape prior modelling. We show that the expressive power of second order GRFs is already sufficient to express simple shapes and spatial relations between them simultaneously. This allows to model and recognise complex shapes as spatial compositions of simpler parts.