Feed-forward Uncertainty Propagation in Belief and Neural Networks
Paper and Code
Nov 01, 2018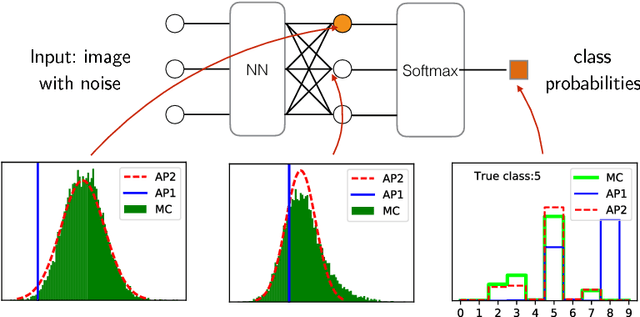
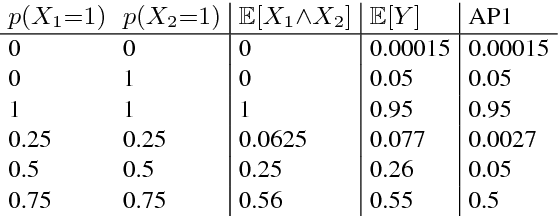
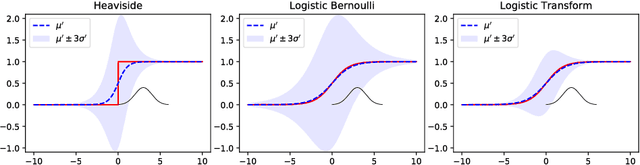
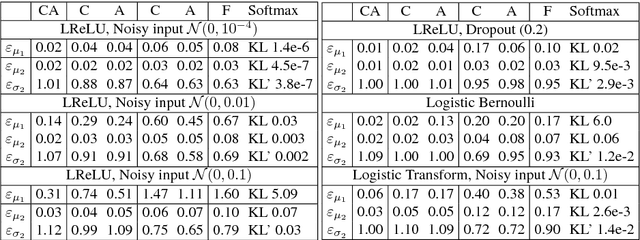
We propose a feed-forward inference method applicable to belief and neural networks. In a belief network, the method estimates an approximate factorized posterior of all hidden units given the input. In neural networks the method propagates uncertainty of the input through all the layers. In neural networks with injected noise, the method analytically takes into account uncertainties resulting from this noise. Such feed-forward analytic propagation is differentiable in parameters and can be trained end-to-end. Compared to standard NN, which can be viewed as propagating only the means, we propagate the mean and variance. The method can be useful in all scenarios that require knowledge of the neuron statistics, e.g. when dealing with uncertain inputs, considering sigmoid activations as probabilities of Bernoulli units, training the models regularized by injected noise (dropout) or estimating activation statistics over the dataset (as needed for normalization methods). In the experiments we show the possible utility of the method in all these tasks as well as its current limitations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge