Minimax deviation strategies for machine learning and recognition with short learning samples

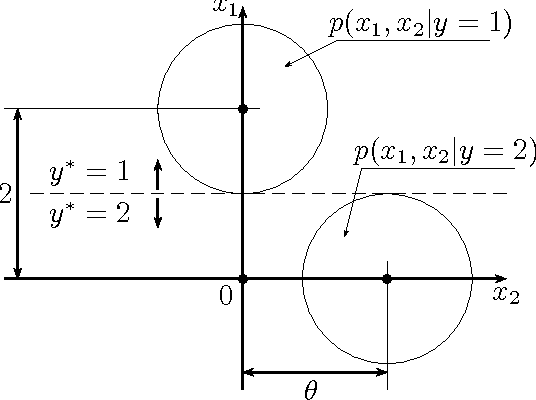
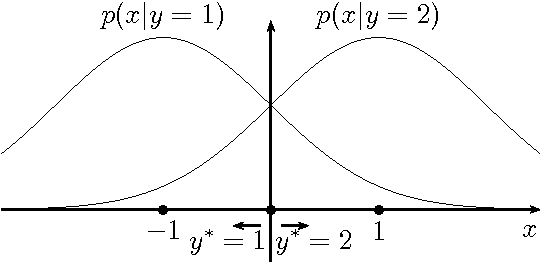
The article is devoted to the problem of small learning samples in machine learning. The flaws of maximum likelihood learning and minimax learning are looked into and the concept of minimax deviation learning is introduced that is free of those flaws.

How to Formulate and Solve Statistical Recognition and Learning Problems

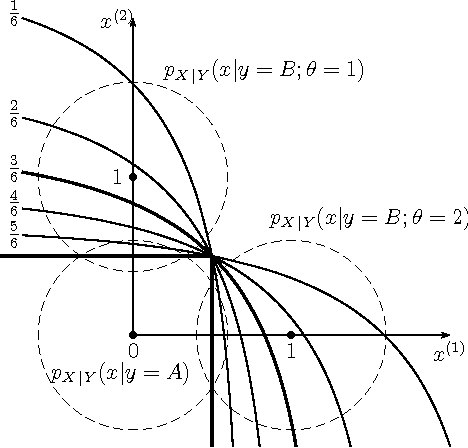
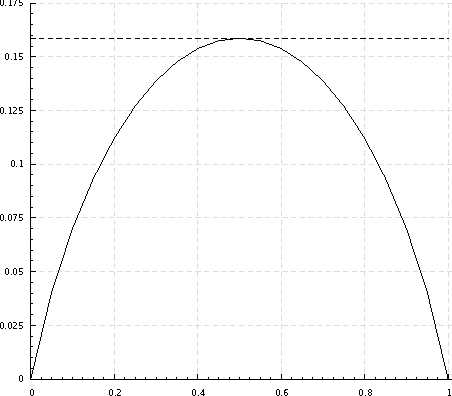
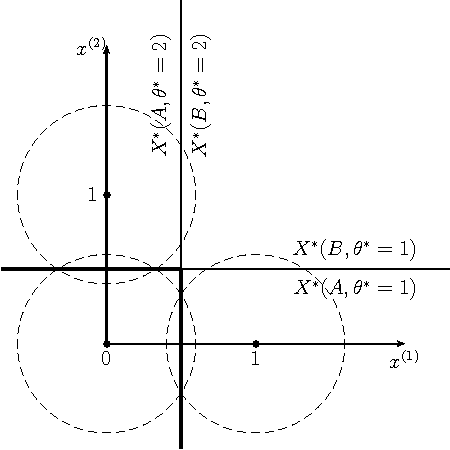
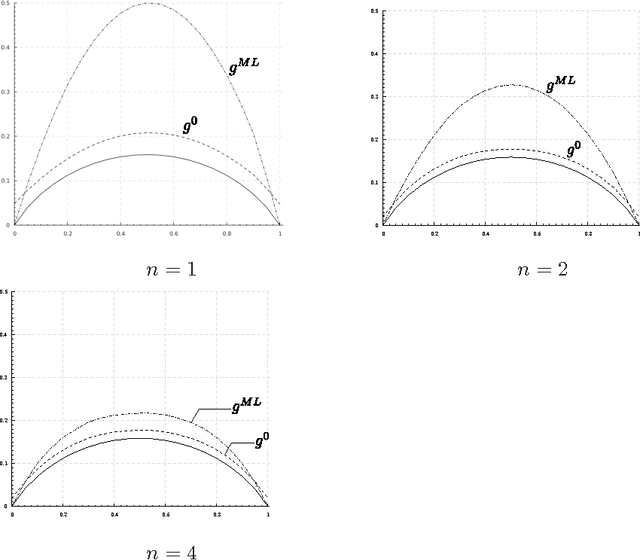
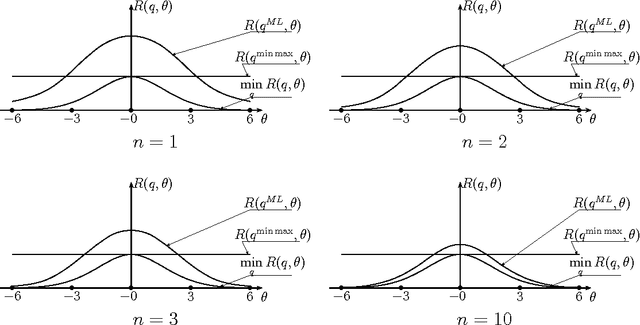
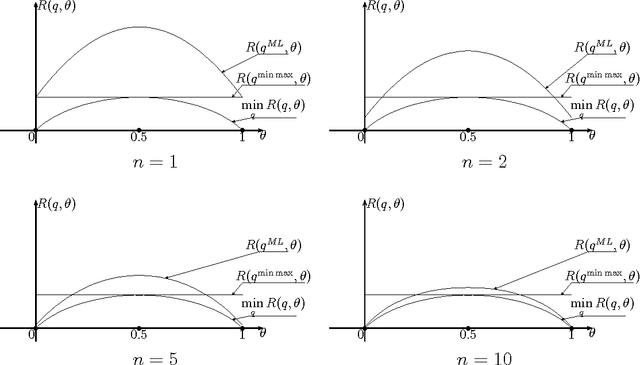
We formulate problems of statistical recognition and learning in a common framework of complex hypothesis testing. Based on arguments from multi-criteria optimization, we identify strategies that are improper for solving these problems and derive a common form of the remaining strategies. We show that some widely used approaches to recognition and learning are improper in this sense. We then propose a generalized formulation of the recognition and learning problem which embraces the whole range of sizes of the learning sample, including the zero size. Learning becomes a special case of recognition without learning. We define the concept of closest to optimal strategy, being a solution to the formulated problem, and describe a technique for finding such a strategy. On several illustrative cases, the strategy is shown to be superior to the widely used learning methods based on maximal likelihood estimation.

M-best solutions for a class of fuzzy constraint satisfaction problems

The article considers one of the possible generalizations of constraint satisfaction problems where relations are replaced by multivalued membership functions. In this case operations of disjunction and conjunction are replaced by maximum and minimum, and consistency of a solution becomes multivalued rather than binary. The article studies the problem of finding d most admissible solutions for a given d. A tractable subclass of these problems is defined by the concepts of invariants and polymorphisms similar to the classic constraint satisfaction approach. These concepts are adapted in two ways. Firstly, the correspondence of "invariant-polymorphism" is generalized to (min,max) semirings. Secondly, we consider non-uniform polymorphisms, where each variable has its own operator, in contrast to the case of one operator common for all variables. The article describes an algorithm that finds $d$ most admissible solutions in polynomial time, provided that the problem is invariant with respect to some non-uniform majority operator. It is essential that this operator needs not to be known for the algorithm to work. Moreover, even a guarantee for the existence of such an operator is not necessary. The algorithm either finds the solution or discards the problem. The latter is possible only if the problem has no majority polymorphism.