How to Formulate and Solve Statistical Recognition and Learning Problems
Paper and Code
Sep 29, 2015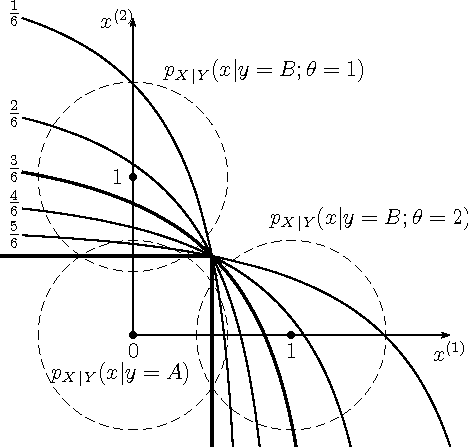
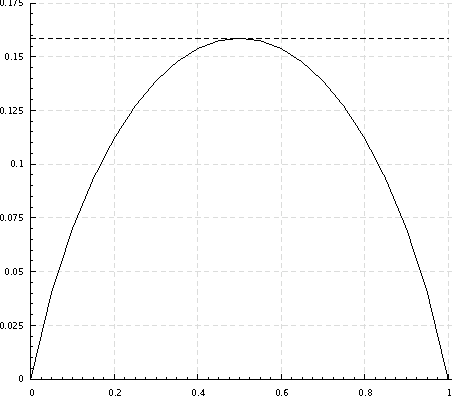
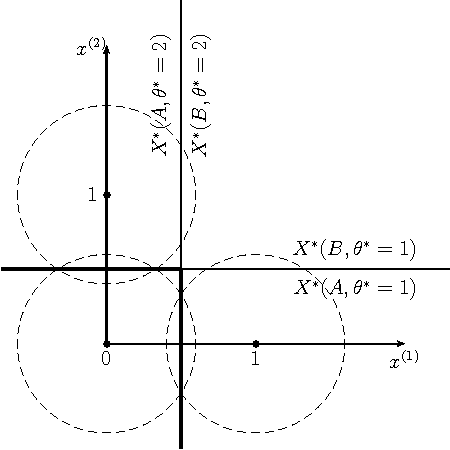
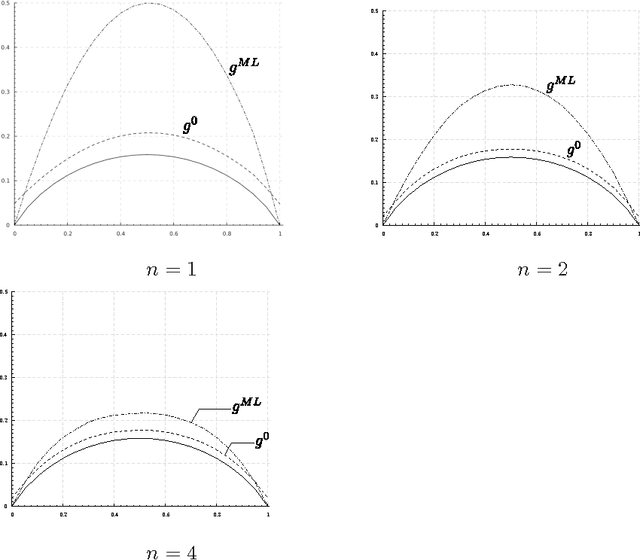
We formulate problems of statistical recognition and learning in a common framework of complex hypothesis testing. Based on arguments from multi-criteria optimization, we identify strategies that are improper for solving these problems and derive a common form of the remaining strategies. We show that some widely used approaches to recognition and learning are improper in this sense. We then propose a generalized formulation of the recognition and learning problem which embraces the whole range of sizes of the learning sample, including the zero size. Learning becomes a special case of recognition without learning. We define the concept of closest to optimal strategy, being a solution to the formulated problem, and describe a technique for finding such a strategy. On several illustrative cases, the strategy is shown to be superior to the widely used learning methods based on maximal likelihood estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge