Reintroducing Straight-Through Estimators as Principled Methods for Stochastic Binary Networks

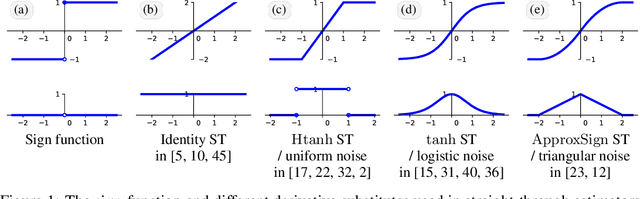
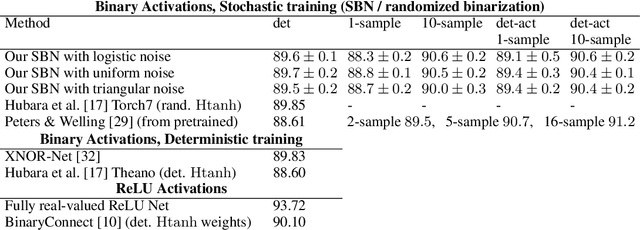
Training neural networks with binary weights and activations is a challenging problem due to the lack of gradients and difficulty of optimization over discrete weights. Many successful experimental results have been recently achieved using the empirical straight-through estimation approach. This approach has generated a variety of ad-hoc rules for propagating gradients through non-differentiable activations and updating discrete weights. We put such methods on a solid basis by obtaining them as viable approximations in the stochastic binary network (SBN) model with Bernoulli weights. In this model gradients are well-defined and the weight probabilities can be optimized by continuous techniques. By choosing the activation noises in SBN appropriately and choosing mirror descent (MD) for optimization, we obtain methods that closely resemble several existing straight-through variants, but unlike them, all work reliably and produce equally good results. We further show that variational inference for Bayesian learning of Binary weights can be implemented using MD updates with the same simplicity.

Path Sample-Analytic Gradient Estimators for Stochastic Binary Networks

In networks with binary activations and or binary weights the training by gradient descent is complicated as the model has piecewise constant response. We consider stochastic binary networks, obtained by adding noises in front of activations. The expected model response becomes a smooth function of parameters, its gradient is well defined but is challenging to estimate accurately. We propose a new method for this estimation problem combining sampling and analytic approximation steps. The method has a significantly reduced variance at the price of a small bias which gives a very practical tradeoff in comparison with existing unbiased and biased estimators. We further show that one extra linearization step leads to a deep straight-through estimator previously known only as an ad-hoc heuristic. We experimentally show higher accuracy in gradient estimation and demonstrate a more stable and better performing training in deep convolutional models with both proposed methods.

Hamiltonian Monte-Carlo for Orthogonal Matrices

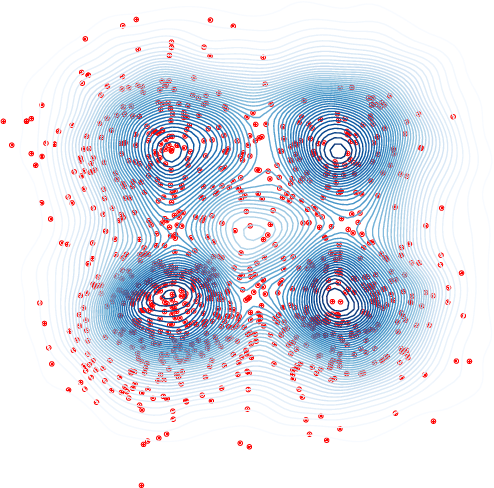
We consider the problem of sampling from posterior distributions for Bayesian models where some parameters are restricted to be orthogonal matrices. Such matrices are sometimes used in neural networks models for reasons of regularization and stabilization of training procedures, and also can parameterize matrices of bounded rank, positive-definite matrices and others. In \citet{byrne2013geodesic} authors have already considered sampling from distributions over manifolds using exact geodesic flows in a scheme similar to Hamiltonian Monte Carlo (HMC). We propose new sampling scheme for a set of orthogonal matrices that is based on the same approach, uses ideas of Riemannian optimization and does not require exact computation of geodesic flows. The method is theoretically justified by proof of symplecticity for the proposed iteration. In experiments we show that the new scheme is comparable or faster in time per iteration and more sample-efficient comparing to conventional HMC with explicit orthogonal parameterization and Geodesic Monte-Carlo. We also provide promising results of Bayesian ensembling for orthogonal neural networks and low-rank matrix factorization.