TEncDM: Understanding the Properties of Diffusion Model in the Space of Language Model Encodings

Drawing inspiration from the success of diffusion models in various domains, numerous research papers proposed methods for adapting them to text data. Despite these efforts, none of them has managed to achieve the quality of the large language models. In this paper, we conduct a comprehensive analysis of key components of the text diffusion models and introduce a novel approach named Text Encoding Diffusion Model (TEncDM). Instead of the commonly used token embedding space, we train our model in the space of the language model encodings. Additionally, we propose to use a Transformer-based decoder that utilizes contextual information for text reconstruction. We also analyse self-conditioning and find that it increases the magnitude of the model outputs, allowing the reduction of the number of denoising steps at the inference stage. Evaluation of TEncDM on two downstream text generation tasks, QQP and XSum, demonstrates its superiority over existing non-autoregressive models.

Star-Shaped Denoising Diffusion Probabilistic Models

Methods based on Denoising Diffusion Probabilistic Models (DDPM) became a ubiquitous tool in generative modeling. However, they are mostly limited to Gaussian and discrete diffusion processes. We propose Star-Shaped Denoising Diffusion Probabilistic Models (SS-DDPM), a model with a non-Markovian diffusion-like noising process. In the case of Gaussian distributions, this model is equivalent to Markovian DDPMs. However, it can be defined and applied with arbitrary noising distributions, and admits efficient training and sampling algorithms for a wide range of distributions that lie in the exponential family. We provide a simple recipe for designing diffusion-like models with distributions like Beta, von Mises--Fisher, Dirichlet, Wishart and others, which can be especially useful when data lies on a constrained manifold such as the unit sphere, the space of positive semi-definite matrices, the probabilistic simplex, etc. We evaluate the model in different settings and find it competitive even on image data, where Beta SS-DDPM achieves results comparable to a Gaussian DDPM.

Reintroducing Straight-Through Estimators as Principled Methods for Stochastic Binary Networks

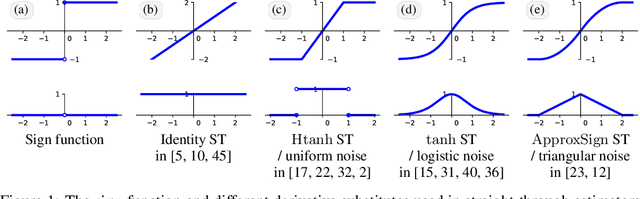
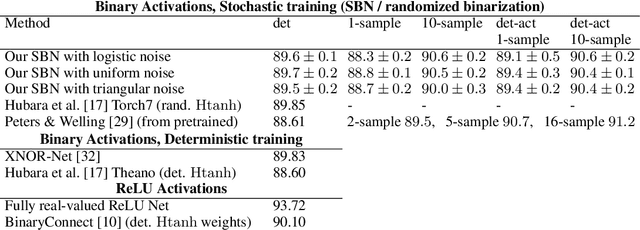
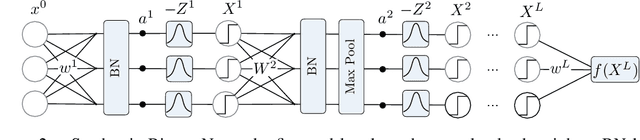
Training neural networks with binary weights and activations is a challenging problem due to the lack of gradients and difficulty of optimization over discrete weights. Many successful experimental results have been recently achieved using the empirical straight-through estimation approach. This approach has generated a variety of ad-hoc rules for propagating gradients through non-differentiable activations and updating discrete weights. We put such methods on a solid basis by obtaining them as viable approximations in the stochastic binary network (SBN) model with Bernoulli weights. In this model gradients are well-defined and the weight probabilities can be optimized by continuous techniques. By choosing the activation noises in SBN appropriately and choosing mirror descent (MD) for optimization, we obtain methods that closely resemble several existing straight-through variants, but unlike them, all work reliably and produce equally good results. We further show that variational inference for Bayesian learning of Binary weights can be implemented using MD updates with the same simplicity.

Greedy Policy Search: A Simple Baseline for Learnable Test-Time Augmentation

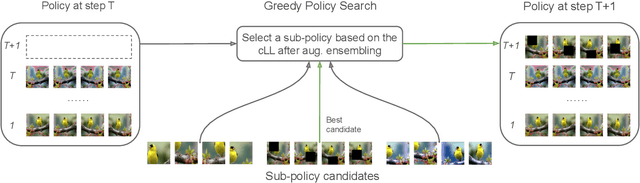
Test-time data augmentation---averaging the predictions of a machine learning model across multiple augmented samples of data---is a widely used technique that improves the predictive performance. While many advanced learnable data augmentation techniques have emerged in recent years, they are focused on the training phase. Such techniques are not necessarily optimal for test-time augmentation and can be outperformed by a policy consisting of simple crops and flips. The primary goal of this paper is to demonstrate that test-time augmentation policies can be successfully learned too. We~introduce \emph{greedy policy search} (GPS), a simple but high-performing method for learning a policy of test-time augmentation. We demonstrate that augmentation policies learned with GPS achieve superior predictive performance on image classification problems, provide better in-domain uncertainty estimation, and improve the robustness to domain shift.

Pitfalls of In-Domain Uncertainty Estimation and Ensembling in Deep Learning

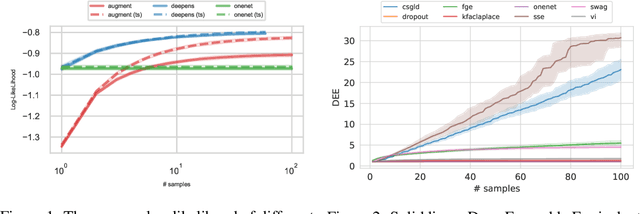
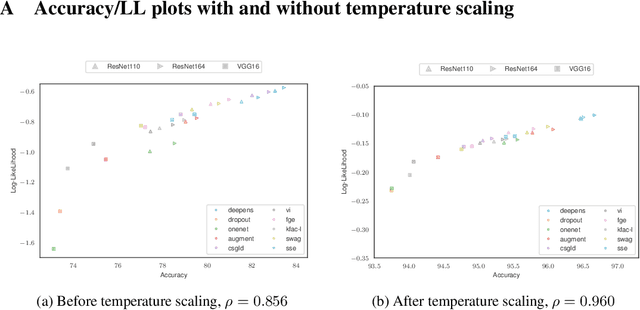
Uncertainty estimation and ensembling methods go hand-in-hand. Uncertainty estimation is one of the main benchmarks for assessment of ensembling performance. At the same time, deep learning ensembles have provided state-of-the-art results in uncertainty estimation. In this work, we focus on in-domain uncertainty for image classification. We explore the standards for its quantification and point out pitfalls of existing metrics. Avoiding these pitfalls, we perform a broad study of different ensembling techniques. To provide more insight in this study, we introduce the deep ensemble equivalent score (DEE) and show that many sophisticated ensembling techniques are equivalent to an ensemble of only few independently trained networks in terms of test performance.

Variational Dropout via Empirical Bayes

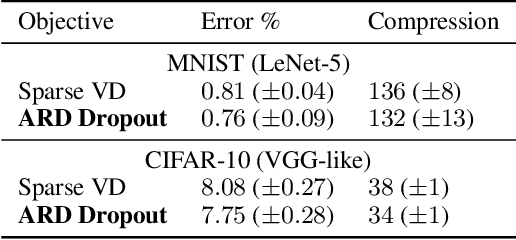
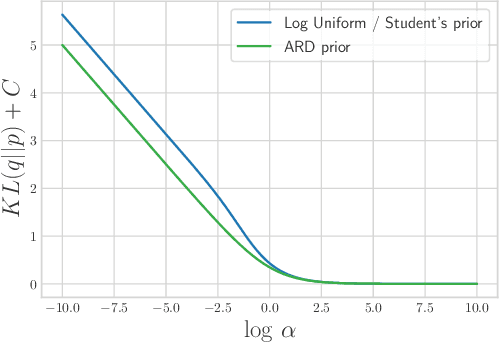
We study the Automatic Relevance Determination procedure applied to deep neural networks. We show that ARD applied to Bayesian DNNs with Gaussian approximate posterior distributions leads to a variational bound similar to that of variational dropout, and in the case of a fixed dropout rate, objectives are exactly the same. Experimental results show that the two approaches yield comparable results in practice even when the dropout rates are trained. This leads to an alternative Bayesian interpretation of dropout and mitigates some of the theoretical issues that arise with the use of improper priors in the variational dropout model. Additionally, we explore the use of the hierarchical priors in ARD and show that it helps achieve higher sparsity for the same accuracy.

Variance Networks: When Expectation Does Not Meet Your Expectations

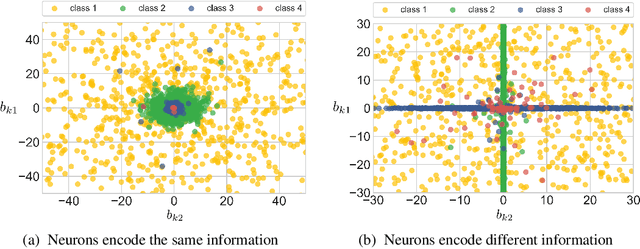
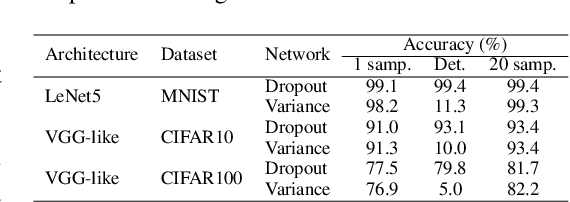
Ordinary stochastic neural networks mostly rely on the expected values of their weights to make predictions, whereas the induced noise is mostly used to capture the uncertainty, prevent overfitting and slightly boost the performance through test-time averaging. In this paper, we introduce variance layers, a different kind of stochastic layers. Each weight of a variance layer follows a zero-mean distribution and is only parameterized by its variance. We show that such layers can learn surprisingly well, can serve as an efficient exploration tool in reinforcement learning tasks and provide a decent defense against adversarial attacks. We also show that a number of conventional Bayesian neural networks naturally converge to such zero-mean posteriors. We observe that in these cases such zero-mean parameterization leads to a much better training objective than conventional parameterizations where the mean is being learned.

Bayesian Incremental Learning for Deep Neural Networks

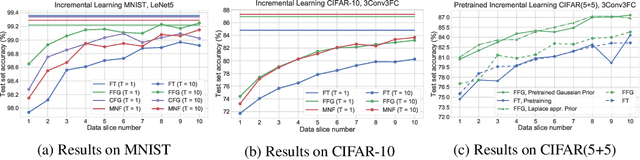
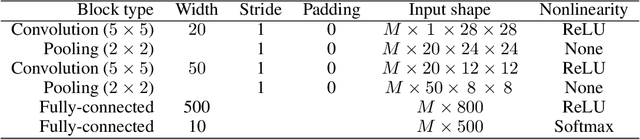
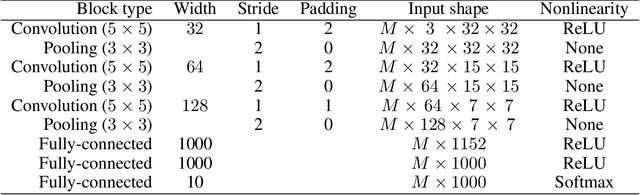
In industrial machine learning pipelines, data often arrive in parts. Particularly in the case of deep neural networks, it may be too expensive to train the model from scratch each time, so one would rather use a previously learned model and the new data to improve performance. However, deep neural networks are prone to getting stuck in a suboptimal solution when trained on only new data as compared to the full dataset. Our work focuses on a continuous learning setup where the task is always the same and new parts of data arrive sequentially. We apply a Bayesian approach to update the posterior approximation with each new piece of data and find this method to outperform the traditional approach in our experiments.

Uncertainty Estimation via Stochastic Batch Normalization

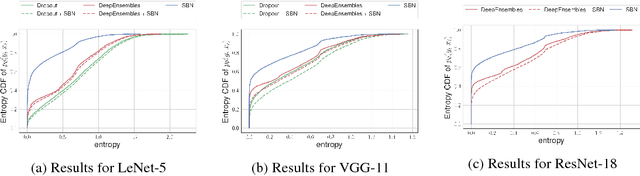
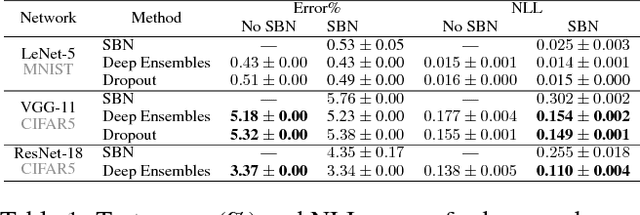
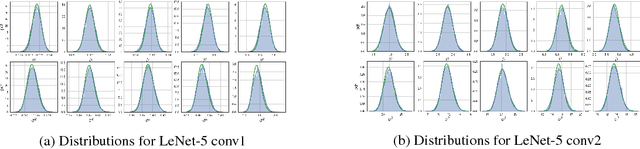
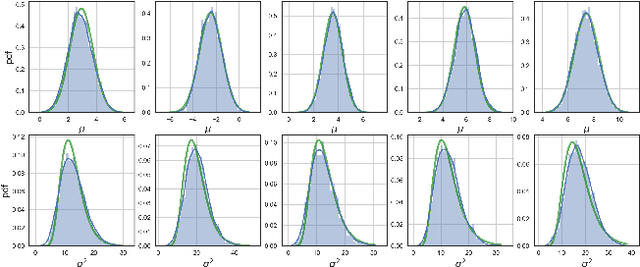
In this work, we investigate Batch Normalization technique and propose its probabilistic interpretation. We propose a probabilistic model and show that Batch Normalization maximazes the lower bound of its marginalized log-likelihood. Then, according to the new probabilistic model, we design an algorithm which acts consistently during train and test. However, inference becomes computationally inefficient. To reduce memory and computational cost, we propose Stochastic Batch Normalization -- an efficient approximation of proper inference procedure. This method provides us with a scalable uncertainty estimation technique. We demonstrate the performance of Stochastic Batch Normalization on popular architectures (including deep convolutional architectures: VGG-like and ResNets) for MNIST and CIFAR-10 datasets.

Structured Bayesian Pruning via Log-Normal Multiplicative Noise

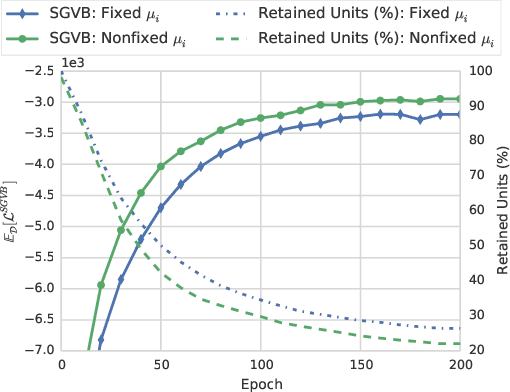
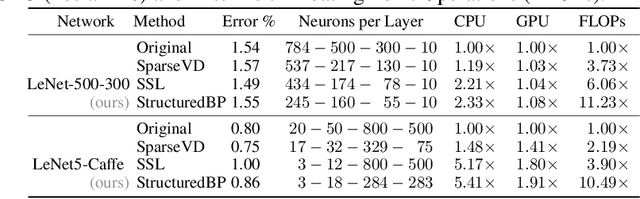
Dropout-based regularization methods can be regarded as injecting random noise with pre-defined magnitude to different parts of the neural network during training. It was recently shown that Bayesian dropout procedure not only improves generalization but also leads to extremely sparse neural architectures by automatically setting the individual noise magnitude per weight. However, this sparsity can hardly be used for acceleration since it is unstructured. In the paper, we propose a new Bayesian model that takes into account the computational structure of neural networks and provides structured sparsity, e.g. removes neurons and/or convolutional channels in CNNs. To do this we inject noise to the neurons outputs while keeping the weights unregularized. We establish the probabilistic model with a proper truncated log-uniform prior over the noise and truncated log-normal variational approximation that ensures that the KL-term in the evidence lower bound is computed in closed-form. The model leads to structured sparsity by removing elements with a low SNR from the computation graph and provides significant acceleration on a number of deep neural architectures. The model is easy to implement as it can be formulated as a separate dropout-like layer.