Bayesian Incremental Learning for Deep Neural Networks

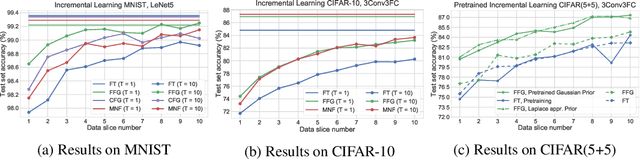
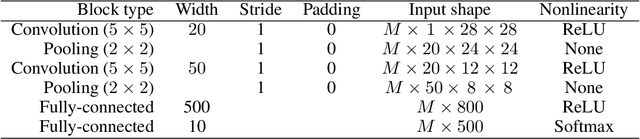
In industrial machine learning pipelines, data often arrive in parts. Particularly in the case of deep neural networks, it may be too expensive to train the model from scratch each time, so one would rather use a previously learned model and the new data to improve performance. However, deep neural networks are prone to getting stuck in a suboptimal solution when trained on only new data as compared to the full dataset. Our work focuses on a continuous learning setup where the task is always the same and new parts of data arrive sequentially. We apply a Bayesian approach to update the posterior approximation with each new piece of data and find this method to outperform the traditional approach in our experiments.

Ultimate tensorization: compressing convolutional and FC layers alike

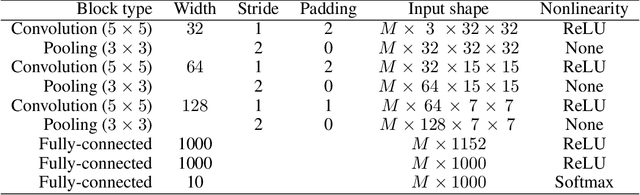
Convolutional neural networks excel in image recognition tasks, but this comes at the cost of high computational and memory complexity. To tackle this problem, [1] developed a tensor factorization framework to compress fully-connected layers. In this paper, we focus on compressing convolutional layers. We show that while the direct application of the tensor framework [1] to the 4-dimensional kernel of convolution does compress the layer, we can do better. We reshape the convolutional kernel into a tensor of higher order and factorize it. We combine the proposed approach with the previous work to compress both convolutional and fully-connected layers of a network and achieve 80x network compression rate with 1.1% accuracy drop on the CIFAR-10 dataset.

Tensorizing Neural Networks

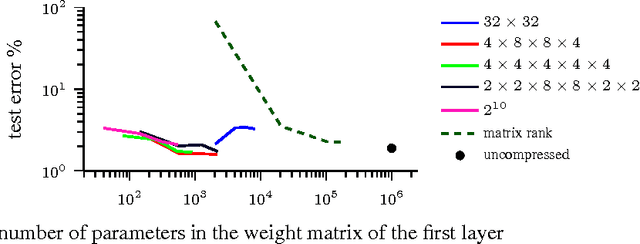
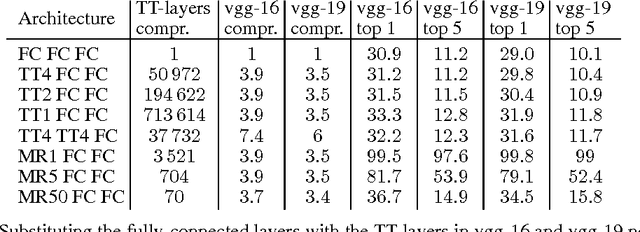
Deep neural networks currently demonstrate state-of-the-art performance in several domains. At the same time, models of this class are very demanding in terms of computational resources. In particular, a large amount of memory is required by commonly used fully-connected layers, making it hard to use the models on low-end devices and stopping the further increase of the model size. In this paper we convert the dense weight matrices of the fully-connected layers to the Tensor Train format such that the number of parameters is reduced by a huge factor and at the same time the expressive power of the layer is preserved. In particular, for the Very Deep VGG networks we report the compression factor of the dense weight matrix of a fully-connected layer up to 200000 times leading to the compression factor of the whole network up to 7 times.