Reintroducing Straight-Through Estimators as Principled Methods for Stochastic Binary Networks

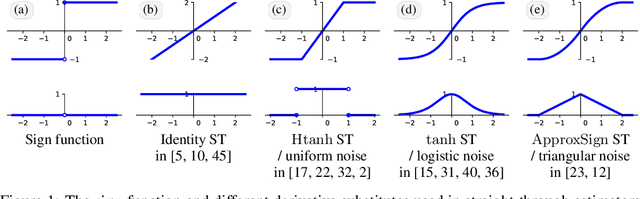
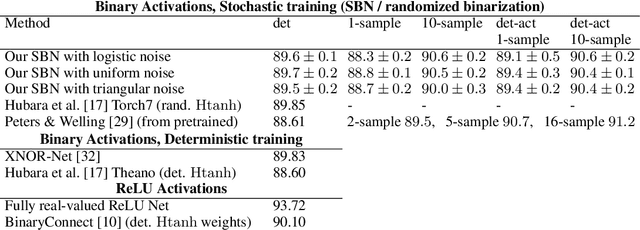
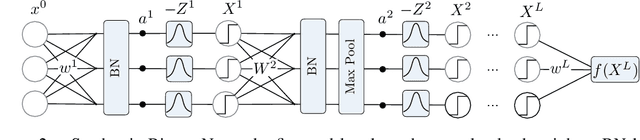
Training neural networks with binary weights and activations is a challenging problem due to the lack of gradients and difficulty of optimization over discrete weights. Many successful experimental results have been recently achieved using the empirical straight-through estimation approach. This approach has generated a variety of ad-hoc rules for propagating gradients through non-differentiable activations and updating discrete weights. We put such methods on a solid basis by obtaining them as viable approximations in the stochastic binary network (SBN) model with Bernoulli weights. In this model gradients are well-defined and the weight probabilities can be optimized by continuous techniques. By choosing the activation noises in SBN appropriately and choosing mirror descent (MD) for optimization, we obtain methods that closely resemble several existing straight-through variants, but unlike them, all work reliably and produce equally good results. We further show that variational inference for Bayesian learning of Binary weights can be implemented using MD updates with the same simplicity.