Valery Kharitonov
Variational Dropout via Empirical Bayes
Nov 01, 2018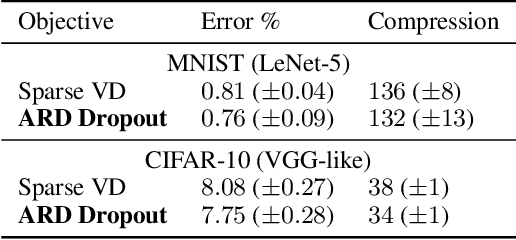
Abstract:We study the Automatic Relevance Determination procedure applied to deep neural networks. We show that ARD applied to Bayesian DNNs with Gaussian approximate posterior distributions leads to a variational bound similar to that of variational dropout, and in the case of a fixed dropout rate, objectives are exactly the same. Experimental results show that the two approaches yield comparable results in practice even when the dropout rates are trained. This leads to an alternative Bayesian interpretation of dropout and mitigates some of the theoretical issues that arise with the use of improper priors in the variational dropout model. Additionally, we explore the use of the hierarchical priors in ARD and show that it helps achieve higher sparsity for the same accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge