Uncertainty Estimation via Stochastic Batch Normalization
Paper and Code
Mar 20, 2018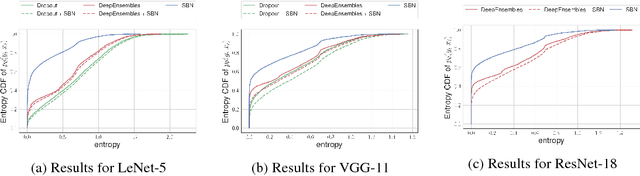
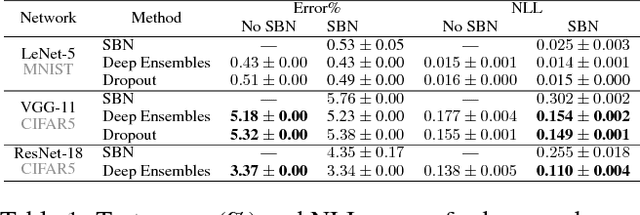
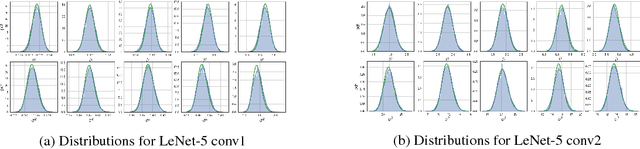
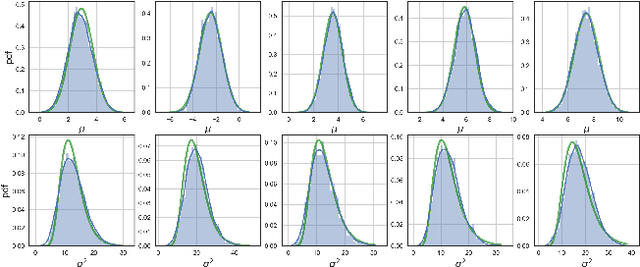
In this work, we investigate Batch Normalization technique and propose its probabilistic interpretation. We propose a probabilistic model and show that Batch Normalization maximazes the lower bound of its marginalized log-likelihood. Then, according to the new probabilistic model, we design an algorithm which acts consistently during train and test. However, inference becomes computationally inefficient. To reduce memory and computational cost, we propose Stochastic Batch Normalization -- an efficient approximation of proper inference procedure. This method provides us with a scalable uncertainty estimation technique. We demonstrate the performance of Stochastic Batch Normalization on popular architectures (including deep convolutional architectures: VGG-like and ResNets) for MNIST and CIFAR-10 datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge