Machine Learning Methods for Spectral Efficiency Prediction in Massive MIMO Systems

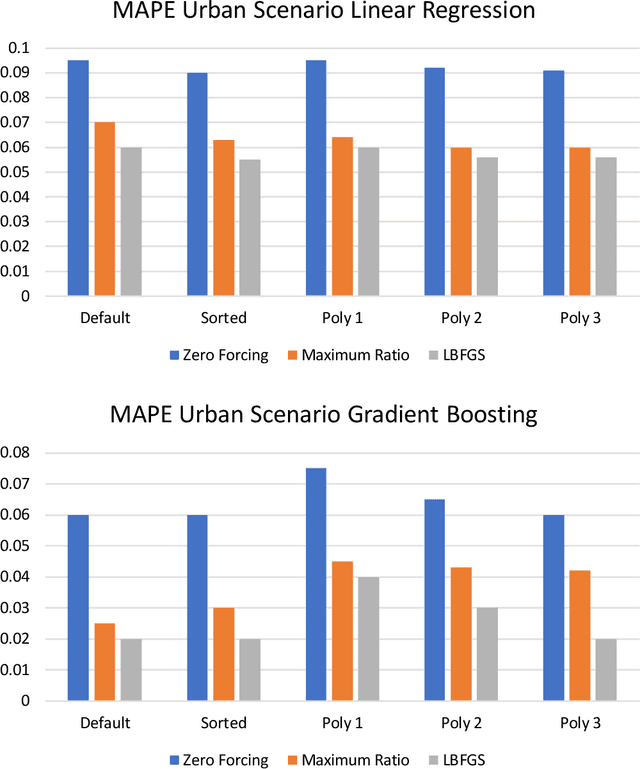
Channel decoding, channel detection, channel assessment, and resource management for wireless multiple-input multiple-output (MIMO) systems are all examples of problems where machine learning (ML) can be successfully applied. In this paper, we study several ML approaches to solve the problem of estimating the spectral efficiency (SE) value for a certain precoding scheme, preferably in the shortest possible time. The best results in terms of mean average percentage error (MAPE) are obtained with gradient boosting over sorted features, while linear models demonstrate worse prediction quality. Neural networks perform similarly to gradient boosting, but they are more resource- and time-consuming because of hyperparameter tuning and frequent retraining. We investigate the practical applicability of the proposed algorithms in a wide range of scenarios generated by the Quadriga simulator. In almost all scenarios, the MAPE achieved using gradient boosting and neural networks is less than 10\%.

Massive MIMO Adaptive Modulation and Coding Using Online Deep Learning

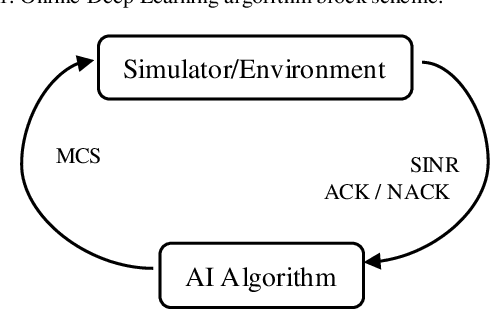
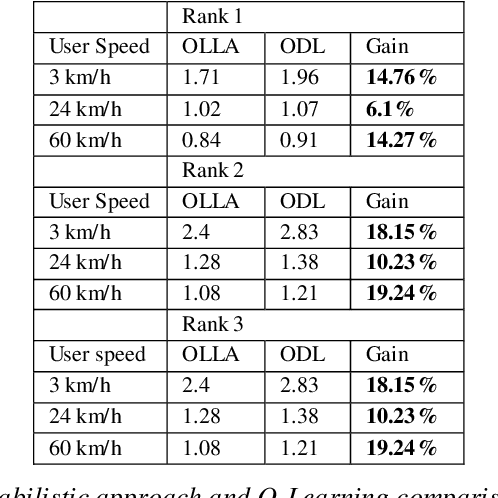
The paper describes an online deep learning algorithm for the adaptive modulation and coding in 5G Massive MIMO. The algorithm is based on a fully connected neural network, which is initially trained on the output of the traditional algorithm and then is incrementally retrained by the service feedback of its output. We show the advantage of our solution over the state-of-the-art Q-Learning approach. We provide system-level simulation results to support this conclusion in various scenarios with different channel characteristics and different user speeds. Compared with traditional OLLA our algorithm shows 10% to 20% improvement of user throughput in full buffer case.

MARS: Masked Automatic Ranks Selection in Tensor Decompositions

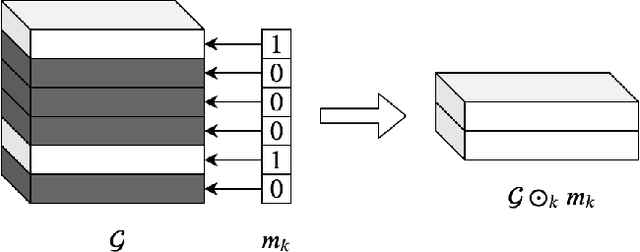
Tensor decomposition methods have recently proven to be efficient for compressing and accelerating neural networks. However, the problem of optimal decomposition structure determination is still not well studied while being quite important. Specifically, decomposition ranks present the crucial parameter controlling the compression-accuracy trade-off. In this paper, we introduce MARS -- a new efficient method for the automatic selection of ranks in general tensor decompositions. During training, the procedure learns binary masks over decomposition cores that "select" the optimal tensor structure. The learning is performed via relaxed maximum a posteriori (MAP) estimation in a specific Bayesian model. The proposed method achieves better results compared to previous works in various tasks.

Hamiltonian Monte-Carlo for Orthogonal Matrices

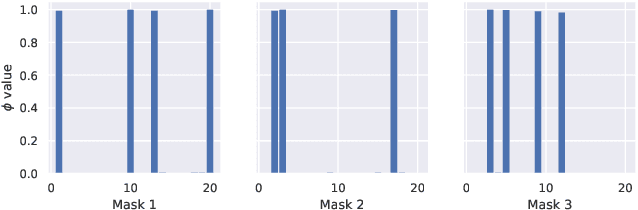
We consider the problem of sampling from posterior distributions for Bayesian models where some parameters are restricted to be orthogonal matrices. Such matrices are sometimes used in neural networks models for reasons of regularization and stabilization of training procedures, and also can parameterize matrices of bounded rank, positive-definite matrices and others. In \citet{byrne2013geodesic} authors have already considered sampling from distributions over manifolds using exact geodesic flows in a scheme similar to Hamiltonian Monte Carlo (HMC). We propose new sampling scheme for a set of orthogonal matrices that is based on the same approach, uses ideas of Riemannian optimization and does not require exact computation of geodesic flows. The method is theoretically justified by proof of symplecticity for the proposed iteration. In experiments we show that the new scheme is comparable or faster in time per iteration and more sample-efficient comparing to conventional HMC with explicit orthogonal parameterization and Geodesic Monte-Carlo. We also provide promising results of Bayesian ensembling for orthogonal neural networks and low-rank matrix factorization.

Scalable Gaussian Processes with Billions of Inducing Inputs via Tensor Train Decomposition

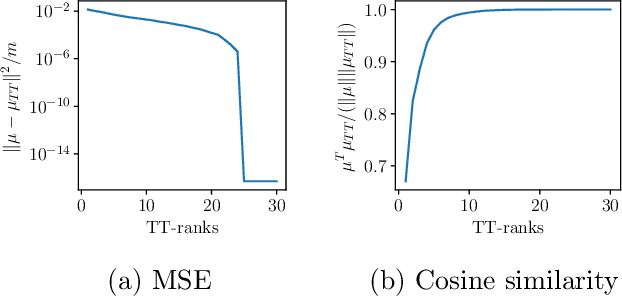
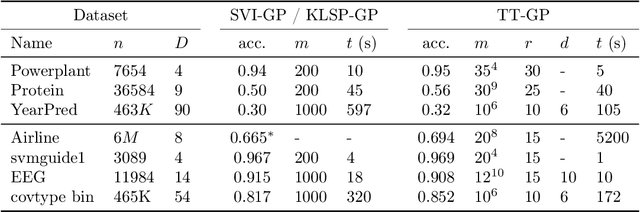
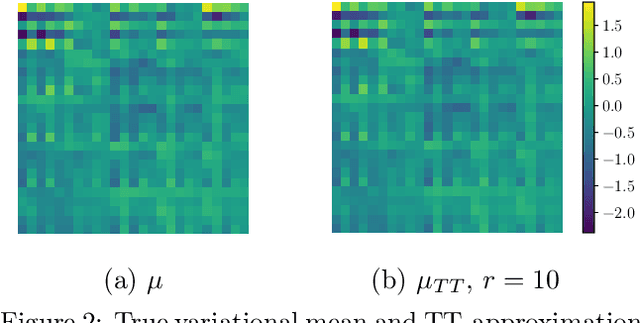
We propose a method (TT-GP) for approximate inference in Gaussian Process (GP) models. We build on previous scalable GP research including stochastic variational inference based on inducing inputs, kernel interpolation, and structure exploiting algebra. The key idea of our method is to use Tensor Train decomposition for variational parameters, which allows us to train GPs with billions of inducing inputs and achieve state-of-the-art results on several benchmarks. Further, our approach allows for training kernels based on deep neural networks without any modifications to the underlying GP model. A neural network learns a multidimensional embedding for the data, which is used by the GP to make the final prediction. We train GP and neural network parameters end-to-end without pretraining, through maximization of GP marginal likelihood. We show the efficiency of the proposed approach on several regression and classification benchmark datasets including MNIST, CIFAR-10, and Airline.

Faster variational inducing input Gaussian process classification

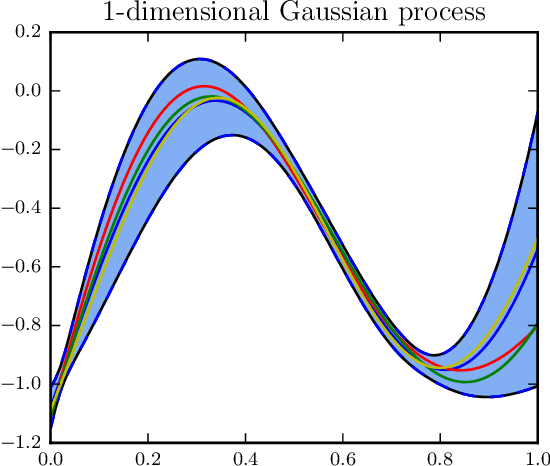
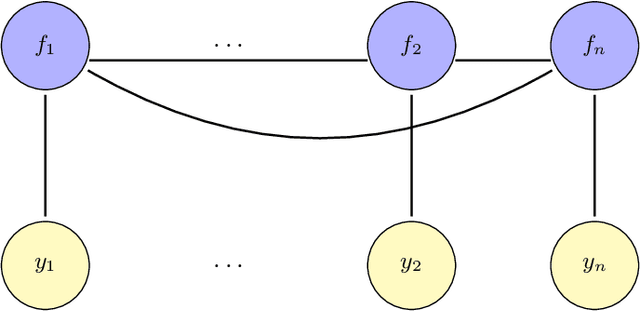
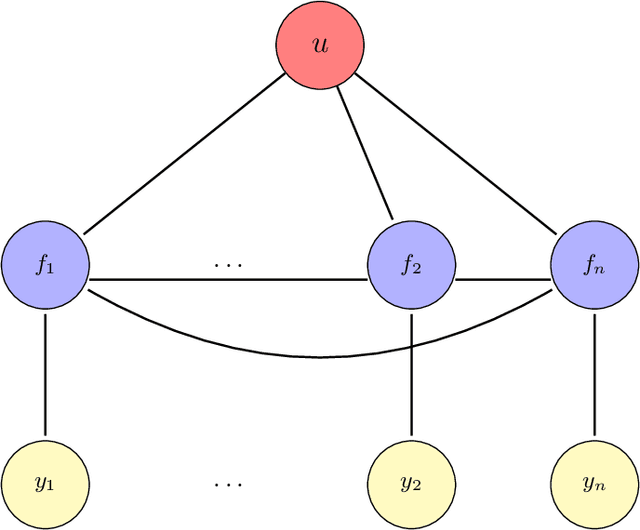
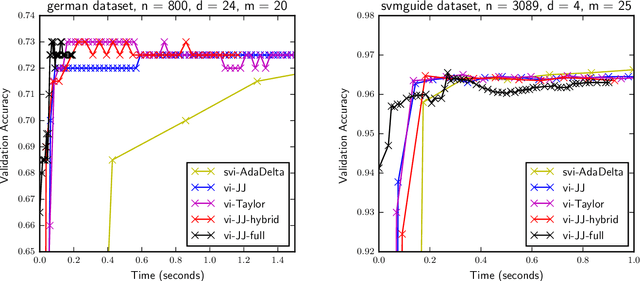
Gaussian processes (GP) provide a prior over functions and allow finding complex regularities in data. Gaussian processes are successfully used for classification/regression problems and dimensionality reduction. In this work we consider the classification problem only. The complexity of standard methods for GP-classification scales cubically with the size of the training dataset. This complexity makes them inapplicable to big data problems. Therefore, a variety of methods were introduced to overcome this limitation. In the paper we focus on methods based on so called inducing inputs. This approach is based on variational inference and proposes a particular lower bound for marginal likelihood (evidence). This bound is then maximized w.r.t. parameters of kernel function of the Gaussian process, thus fitting the model to data. The computational complexity of this method is $O(nm^2)$, where $m$ is the number of inducing inputs used by the model and is assumed to be substantially smaller than the size of the dataset $n$. Recently, a new evidence lower bound for GP-classification problem was introduced. It allows using stochastic optimization, which makes it suitable for big data problems. However, the new lower bound depends on $O(m^2)$ variational parameter, which makes optimization challenging in case of big m. In this work we develop a new approach for training inducing input GP models for classification problems. Here we use quadratic approximation of several terms in the aforementioned evidence lower bound, obtaining analytical expressions for optimal values of most of the parameters in the optimization, thus sufficiently reducing the dimension of optimization space. In our experiments we achieve as well or better results, compared to the existing method. Moreover, our method doesn't require the user to manually set the learning rate, making it more practical, than the existing method.