Faster variational inducing input Gaussian process classification
Paper and Code
Nov 18, 2016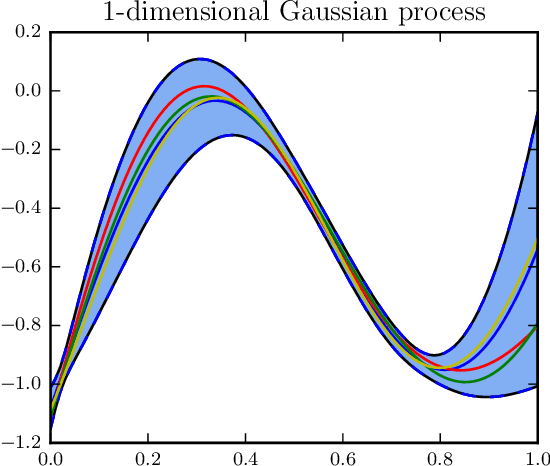
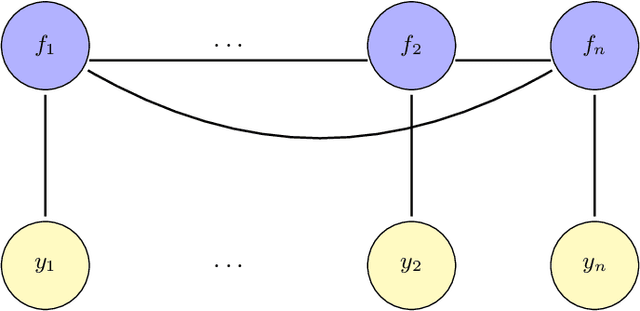
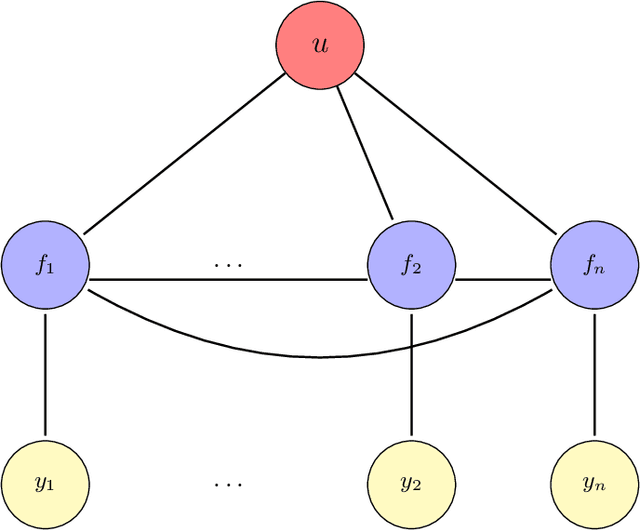
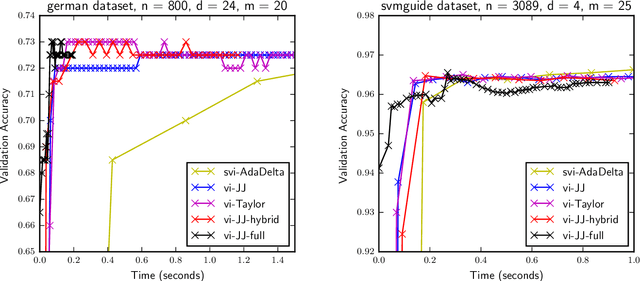
Gaussian processes (GP) provide a prior over functions and allow finding complex regularities in data. Gaussian processes are successfully used for classification/regression problems and dimensionality reduction. In this work we consider the classification problem only. The complexity of standard methods for GP-classification scales cubically with the size of the training dataset. This complexity makes them inapplicable to big data problems. Therefore, a variety of methods were introduced to overcome this limitation. In the paper we focus on methods based on so called inducing inputs. This approach is based on variational inference and proposes a particular lower bound for marginal likelihood (evidence). This bound is then maximized w.r.t. parameters of kernel function of the Gaussian process, thus fitting the model to data. The computational complexity of this method is $O(nm^2)$, where $m$ is the number of inducing inputs used by the model and is assumed to be substantially smaller than the size of the dataset $n$. Recently, a new evidence lower bound for GP-classification problem was introduced. It allows using stochastic optimization, which makes it suitable for big data problems. However, the new lower bound depends on $O(m^2)$ variational parameter, which makes optimization challenging in case of big m. In this work we develop a new approach for training inducing input GP models for classification problems. Here we use quadratic approximation of several terms in the aforementioned evidence lower bound, obtaining analytical expressions for optimal values of most of the parameters in the optimization, thus sufficiently reducing the dimension of optimization space. In our experiments we achieve as well or better results, compared to the existing method. Moreover, our method doesn't require the user to manually set the learning rate, making it more practical, than the existing method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge