Ekaterina Lobacheva
HSE University, Russia
Can Training Dynamics of Scale-Invariant Neural Networks Be Explained by the Thermodynamics of an Ideal Gas?
Nov 10, 2025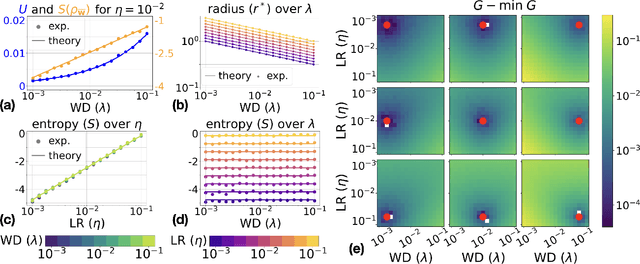

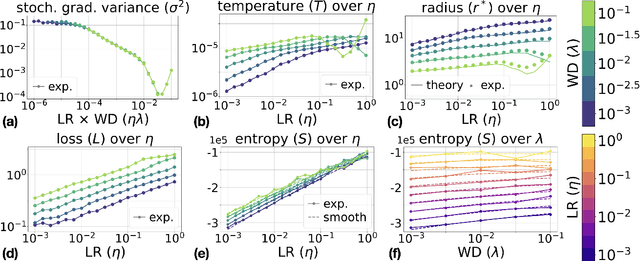

Abstract:Understanding the training dynamics of deep neural networks remains a major open problem, with physics-inspired approaches offering promising insights. Building on this perspective, we develop a thermodynamic framework to describe the stationary distributions of stochastic gradient descent (SGD) with weight decay for scale-invariant neural networks, a setting that both reflects practical architectures with normalization layers and permits theoretical analysis. We establish analogies between training hyperparameters (e.g., learning rate, weight decay) and thermodynamic variables such as temperature, pressure, and volume. Starting with a simplified isotropic noise model, we uncover a close correspondence between SGD dynamics and ideal gas behavior, validated through theory and simulation. Extending to training of neural networks, we show that key predictions of the framework, including the behavior of stationary entropy, align closely with experimental observations. This framework provides a principled foundation for interpreting training dynamics and may guide future work on hyperparameter tuning and the design of learning rate schedulers.
Training Dynamics Underlying Language Model Scaling Laws: Loss Deceleration and Zero-Sum Learning
Jun 05, 2025Abstract:This work aims to understand how scaling improves language models, specifically in terms of training dynamics. We find that language models undergo loss deceleration early in training; an abrupt slowdown in the rate of loss improvement, resulting in piecewise linear behaviour of the loss curve in log-log space. Scaling up the model mitigates this transition by (1) decreasing the loss at which deceleration occurs, and (2) improving the log-log rate of loss improvement after deceleration. We attribute loss deceleration to a type of degenerate training dynamics we term zero-sum learning (ZSL). In ZSL, per-example gradients become systematically opposed, leading to destructive interference in per-example changes in loss. As a result, improving loss on one subset of examples degrades it on another, bottlenecking overall progress. Loss deceleration and ZSL provide new insights into the training dynamics underlying language model scaling laws, and could potentially be targeted directly to improve language models independent of scale. We make our code and artefacts available at: https://github.com/mirandrom/zsl
SGD as Free Energy Minimization: A Thermodynamic View on Neural Network Training
May 29, 2025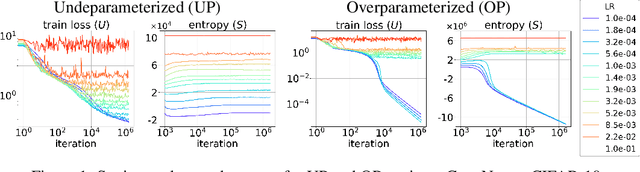

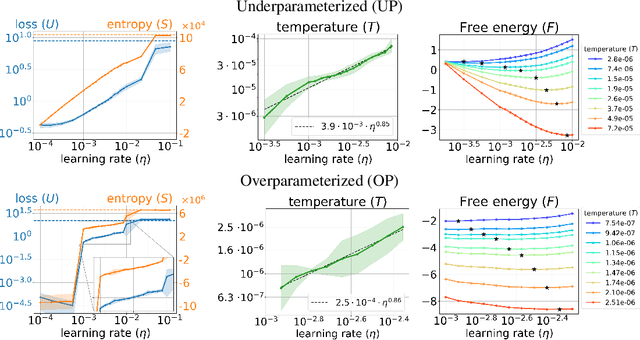
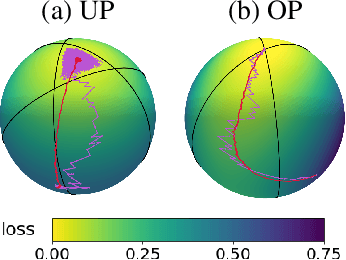
Abstract:We present a thermodynamic interpretation of the stationary behavior of stochastic gradient descent (SGD) under fixed learning rates (LRs) in neural network training. We show that SGD implicitly minimizes a free energy function $F=U-TS$, balancing training loss $U$ and the entropy of the weights distribution $S$, with temperature $T$ determined by the LR. This perspective offers a new lens on why high LRs prevent training from converging to the loss minima and how different LRs lead to stabilization at different loss levels. We empirically validate the free energy framework on both underparameterized (UP) and overparameterized (OP) models. UP models consistently follow free energy minimization, with temperature increasing monotonically with LR, while for OP models, the temperature effectively drops to zero at low LRs, causing SGD to minimize the loss directly and converge to an optimum. We attribute this mismatch to differences in the signal-to-noise ratio of stochastic gradients near optima, supported by both a toy example and neural network experiments.
Where Do Large Learning Rates Lead Us?
Oct 29, 2024



Abstract:It is generally accepted that starting neural networks training with large learning rates (LRs) improves generalization. Following a line of research devoted to understanding this effect, we conduct an empirical study in a controlled setting focusing on two questions: 1) how large an initial LR is required for obtaining optimal quality, and 2) what are the key differences between models trained with different LRs? We discover that only a narrow range of initial LRs slightly above the convergence threshold lead to optimal results after fine-tuning with a small LR or weight averaging. By studying the local geometry of reached minima, we observe that using LRs from this optimal range allows for the optimization to locate a basin that only contains high-quality minima. Additionally, we show that these initial LRs result in a sparse set of learned features, with a clear focus on those most relevant for the task. In contrast, starting training with too small LRs leads to unstable minima and attempts to learn all features simultaneously, resulting in poor generalization. Conversely, using initial LRs that are too large fails to detect a basin with good solutions and extract meaningful patterns from the data.
Large Learning Rates Improve Generalization: But How Large Are We Talking About?
Nov 19, 2023Abstract:Inspired by recent research that recommends starting neural networks training with large learning rates (LRs) to achieve the best generalization, we explore this hypothesis in detail. Our study clarifies the initial LR ranges that provide optimal results for subsequent training with a small LR or weight averaging. We find that these ranges are in fact significantly narrower than generally assumed. We conduct our main experiments in a simplified setup that allows precise control of the learning rate hyperparameter and validate our key findings in a more practical setting.
To Stay or Not to Stay in the Pre-train Basin: Insights on Ensembling in Transfer Learning
Mar 06, 2023Abstract:Transfer learning and ensembling are two popular techniques for improving the performance and robustness of neural networks. Due to the high cost of pre-training, ensembles of models fine-tuned from a single pre-trained checkpoint are often used in practice. Such models end up in the same basin of the loss landscape and thus have limited diversity. In this work, we study if it is possible to improve ensembles trained from a single pre-trained checkpoint by better exploring the pre-train basin or a close vicinity outside of it. We show that while exploration of the pre-train basin may be beneficial for the ensemble, leaving the basin results in losing the benefits of transfer learning and degradation of the ensemble quality.
Training Scale-Invariant Neural Networks on the Sphere Can Happen in Three Regimes
Sep 08, 2022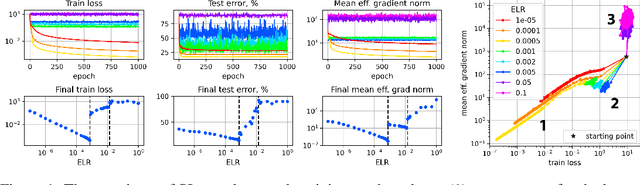

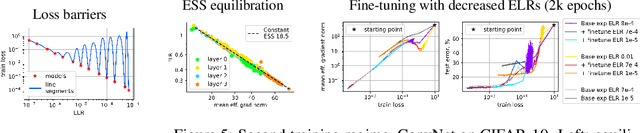

Abstract:A fundamental property of deep learning normalization techniques, such as batch normalization, is making the pre-normalization parameters scale invariant. The intrinsic domain of such parameters is the unit sphere, and therefore their gradient optimization dynamics can be represented via spherical optimization with varying effective learning rate (ELR), which was studied previously. In this work, we investigate the properties of training scale-invariant neural networks directly on the sphere using a fixed ELR. We discover three regimes of such training depending on the ELR value: convergence, chaotic equilibrium, and divergence. We study these regimes in detail both on a theoretical examination of a toy example and on a thorough empirical analysis of real scale-invariant deep learning models. Each regime has unique features and reflects specific properties of the intrinsic loss landscape, some of which have strong parallels with previous research on both regular and scale-invariant neural networks training. Finally, we demonstrate how the discovered regimes are reflected in conventional training of normalized networks and how they can be leveraged to achieve better optima.
Machine Learning Methods for Spectral Efficiency Prediction in Massive MIMO Systems
Dec 29, 2021

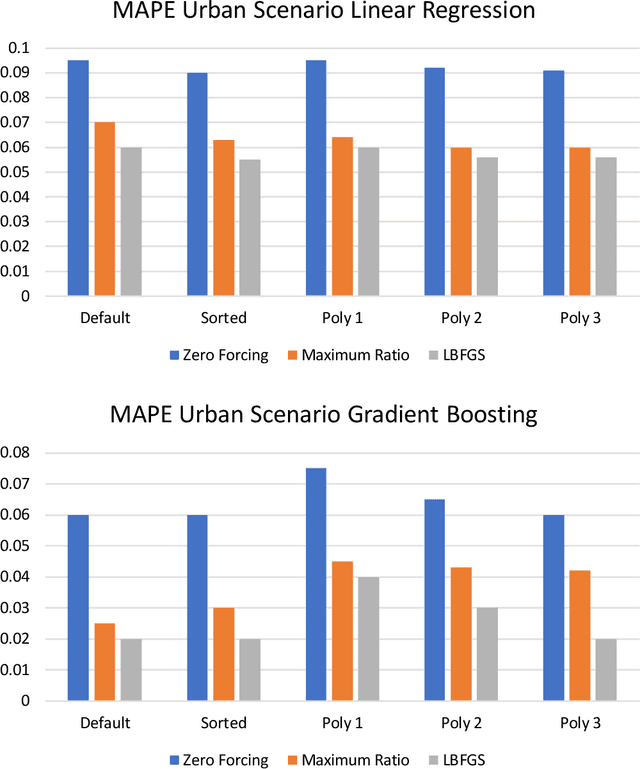
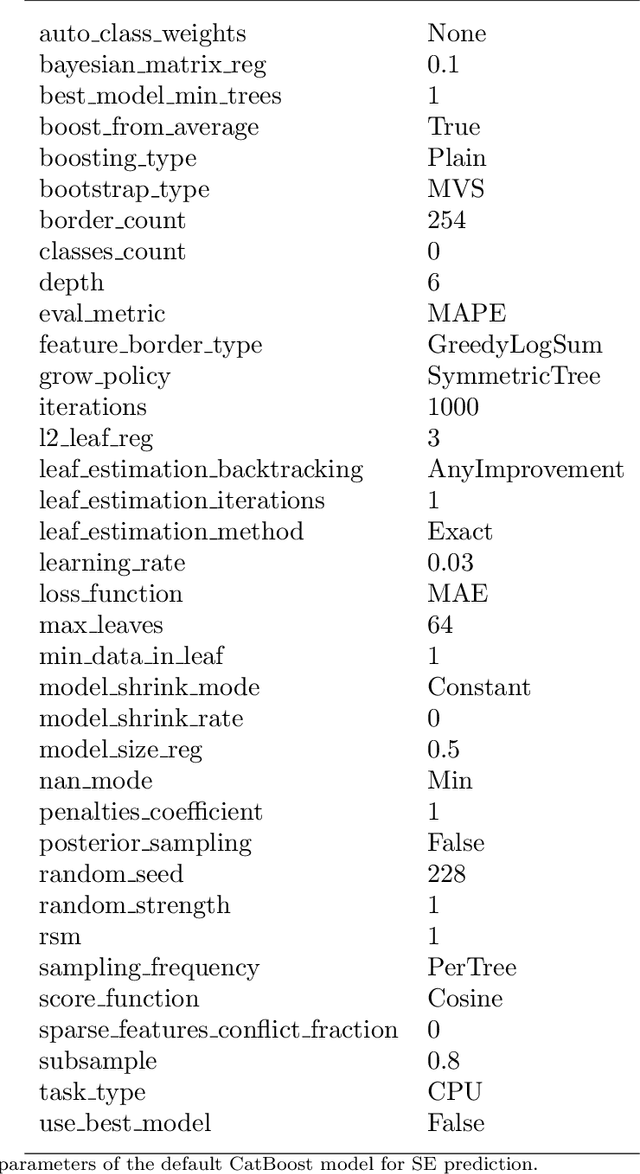
Abstract:Channel decoding, channel detection, channel assessment, and resource management for wireless multiple-input multiple-output (MIMO) systems are all examples of problems where machine learning (ML) can be successfully applied. In this paper, we study several ML approaches to solve the problem of estimating the spectral efficiency (SE) value for a certain precoding scheme, preferably in the shortest possible time. The best results in terms of mean average percentage error (MAPE) are obtained with gradient boosting over sorted features, while linear models demonstrate worse prediction quality. Neural networks perform similarly to gradient boosting, but they are more resource- and time-consuming because of hyperparameter tuning and frequent retraining. We investigate the practical applicability of the proposed algorithms in a wide range of scenarios generated by the Quadriga simulator. In almost all scenarios, the MAPE achieved using gradient boosting and neural networks is less than 10\%.
On the Memorization Properties of Contrastive Learning
Jul 21, 2021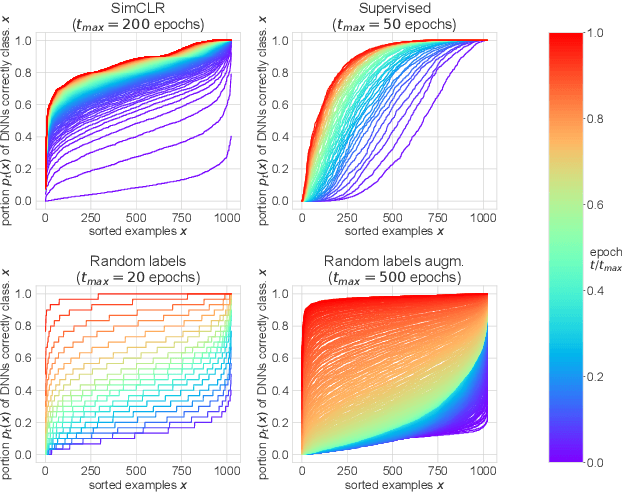
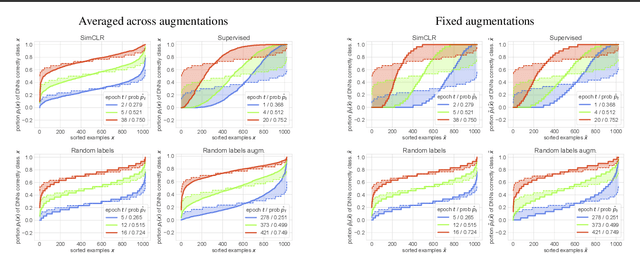
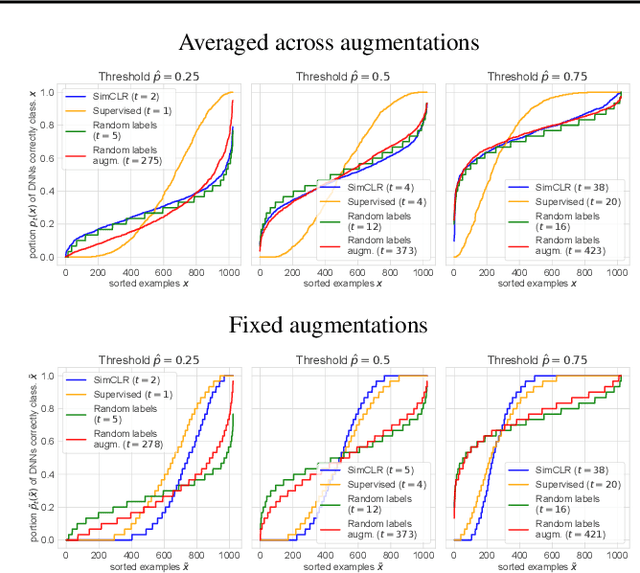
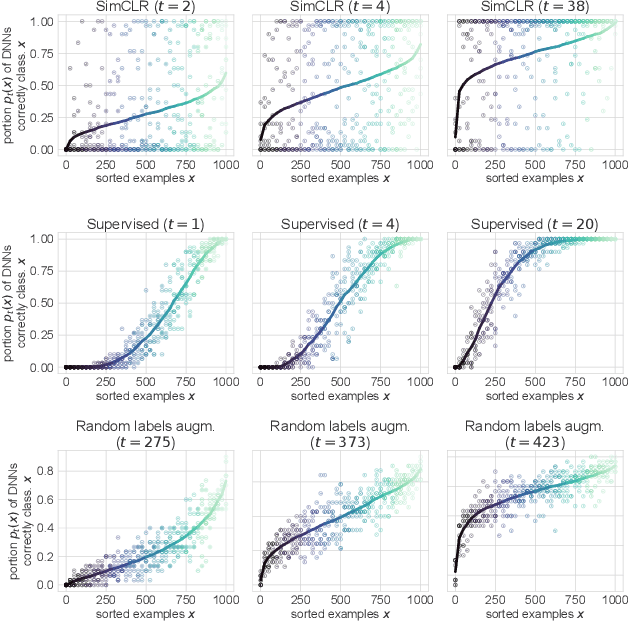
Abstract:Memorization studies of deep neural networks (DNNs) help to understand what patterns and how do DNNs learn, and motivate improvements to DNN training approaches. In this work, we investigate the memorization properties of SimCLR, a widely used contrastive self-supervised learning approach, and compare them to the memorization of supervised learning and random labels training. We find that both training objects and augmentations may have different complexity in the sense of how SimCLR learns them. Moreover, we show that SimCLR is similar to random labels training in terms of the distribution of training objects complexity.
On the Periodic Behavior of Neural Network Training with Batch Normalization and Weight Decay
Jun 29, 2021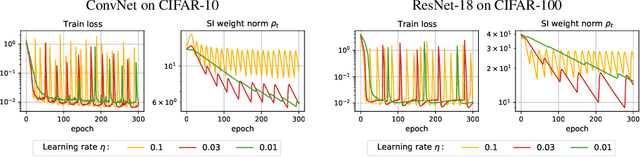

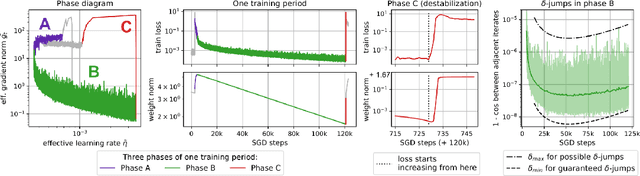
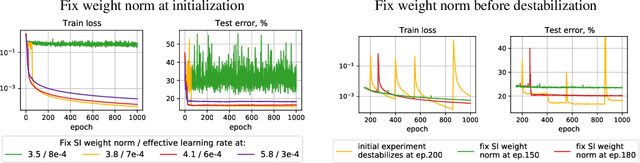
Abstract:Despite the conventional wisdom that using batch normalization with weight decay may improve neural network training, some recent works show their joint usage may cause instabilities at the late stages of training. Other works, in contrast, show convergence to the equilibrium, i.e., the stabilization of training metrics. In this paper, we study this contradiction and show that instead of converging to a stable equilibrium, the training dynamics converge to consistent periodic behavior. That is, the training process regularly exhibits instabilities which, however, do not lead to complete training failure, but cause a new period of training. We rigorously investigate the mechanism underlying this discovered periodic behavior both from an empirical and theoretical point of view and show that this periodic behavior is indeed caused by the interaction between batch normalization and weight decay.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge