On the Periodic Behavior of Neural Network Training with Batch Normalization and Weight Decay
Paper and Code
Jun 29, 2021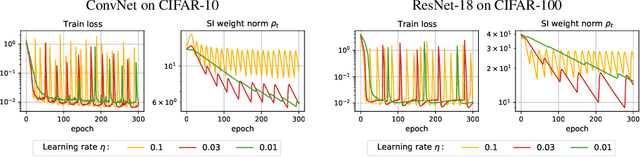

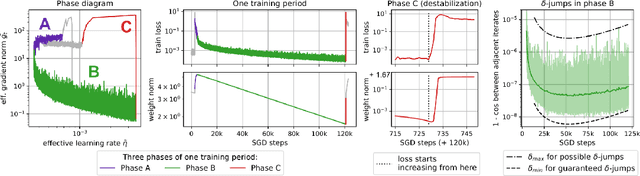
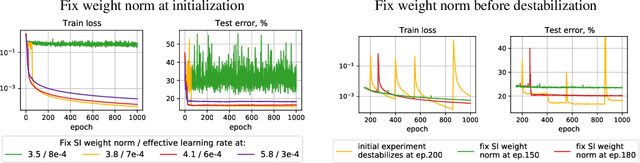
Despite the conventional wisdom that using batch normalization with weight decay may improve neural network training, some recent works show their joint usage may cause instabilities at the late stages of training. Other works, in contrast, show convergence to the equilibrium, i.e., the stabilization of training metrics. In this paper, we study this contradiction and show that instead of converging to a stable equilibrium, the training dynamics converge to consistent periodic behavior. That is, the training process regularly exhibits instabilities which, however, do not lead to complete training failure, but cause a new period of training. We rigorously investigate the mechanism underlying this discovered periodic behavior both from an empirical and theoretical point of view and show that this periodic behavior is indeed caused by the interaction between batch normalization and weight decay.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge