Where Do Large Learning Rates Lead Us?

It is generally accepted that starting neural networks training with large learning rates (LRs) improves generalization. Following a line of research devoted to understanding this effect, we conduct an empirical study in a controlled setting focusing on two questions: 1) how large an initial LR is required for obtaining optimal quality, and 2) what are the key differences between models trained with different LRs? We discover that only a narrow range of initial LRs slightly above the convergence threshold lead to optimal results after fine-tuning with a small LR or weight averaging. By studying the local geometry of reached minima, we observe that using LRs from this optimal range allows for the optimization to locate a basin that only contains high-quality minima. Additionally, we show that these initial LRs result in a sparse set of learned features, with a clear focus on those most relevant for the task. In contrast, starting training with too small LRs leads to unstable minima and attempts to learn all features simultaneously, resulting in poor generalization. Conversely, using initial LRs that are too large fails to detect a basin with good solutions and extract meaningful patterns from the data.

Large Learning Rates Improve Generalization: But How Large Are We Talking About?

Inspired by recent research that recommends starting neural networks training with large learning rates (LRs) to achieve the best generalization, we explore this hypothesis in detail. Our study clarifies the initial LR ranges that provide optimal results for subsequent training with a small LR or weight averaging. We find that these ranges are in fact significantly narrower than generally assumed. We conduct our main experiments in a simplified setup that allows precise control of the learning rate hyperparameter and validate our key findings in a more practical setting.

Training Scale-Invariant Neural Networks on the Sphere Can Happen in Three Regimes

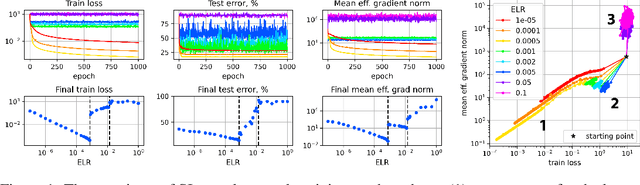
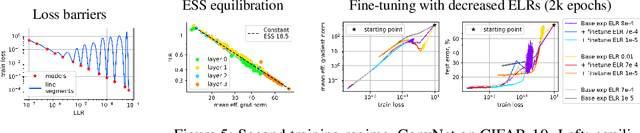
A fundamental property of deep learning normalization techniques, such as batch normalization, is making the pre-normalization parameters scale invariant. The intrinsic domain of such parameters is the unit sphere, and therefore their gradient optimization dynamics can be represented via spherical optimization with varying effective learning rate (ELR), which was studied previously. In this work, we investigate the properties of training scale-invariant neural networks directly on the sphere using a fixed ELR. We discover three regimes of such training depending on the ELR value: convergence, chaotic equilibrium, and divergence. We study these regimes in detail both on a theoretical examination of a toy example and on a thorough empirical analysis of real scale-invariant deep learning models. Each regime has unique features and reflects specific properties of the intrinsic loss landscape, some of which have strong parallels with previous research on both regular and scale-invariant neural networks training. Finally, we demonstrate how the discovered regimes are reflected in conventional training of normalized networks and how they can be leveraged to achieve better optima.

On the Periodic Behavior of Neural Network Training with Batch Normalization and Weight Decay

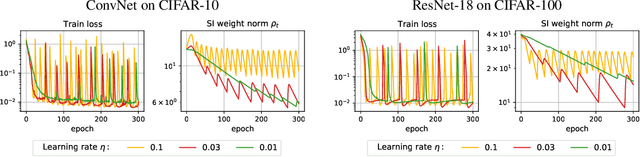
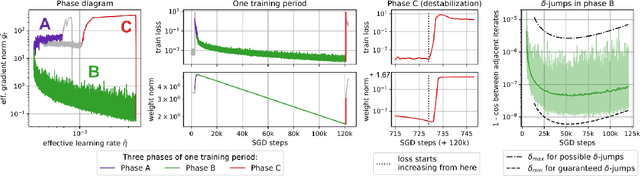
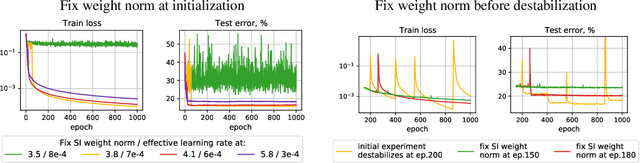
Despite the conventional wisdom that using batch normalization with weight decay may improve neural network training, some recent works show their joint usage may cause instabilities at the late stages of training. Other works, in contrast, show convergence to the equilibrium, i.e., the stabilization of training metrics. In this paper, we study this contradiction and show that instead of converging to a stable equilibrium, the training dynamics converge to consistent periodic behavior. That is, the training process regularly exhibits instabilities which, however, do not lead to complete training failure, but cause a new period of training. We rigorously investigate the mechanism underlying this discovered periodic behavior both from an empirical and theoretical point of view and show that this periodic behavior is indeed caused by the interaction between batch normalization and weight decay.

On Power Laws in Deep Ensembles

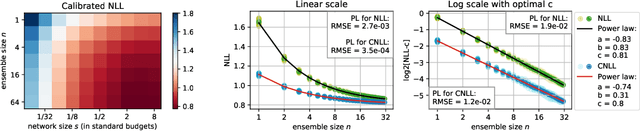
Ensembles of deep neural networks are known to achieve state-of-the-art performance in uncertainty estimation and lead to accuracy improvement. In this work, we focus on a classification problem and investigate the behavior of both non-calibrated and calibrated negative log-likelihood (CNLL) of a deep ensemble as a function of the ensemble size and the member network size. We indicate the conditions under which CNLL follows a power law w.r.t. ensemble size or member network size, and analyze the dynamics of the parameters of the discovered power laws. Our important practical finding is that one large network may perform worse than an ensemble of several medium-size networks with the same total number of parameters (we call this ensemble a memory split). Using the detected power law-like dependencies, we can predict (1) the possible gain from the ensembling of networks with given structure, (2) the optimal memory split given a memory budget, based on a relatively small number of trained networks. We describe the memory split advantage effect in more details in arXiv:2005.07292

MARS: Masked Automatic Ranks Selection in Tensor Decompositions

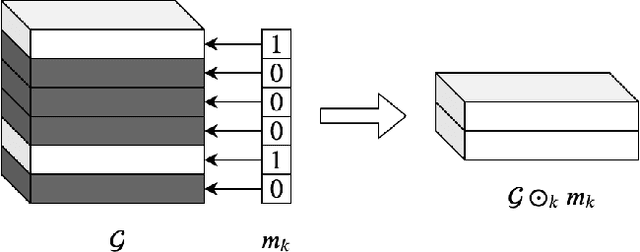
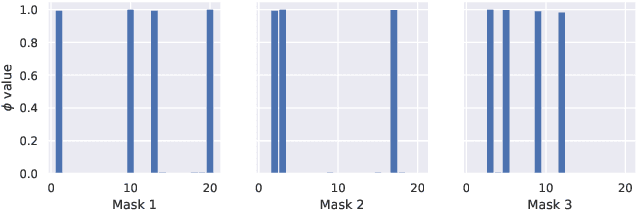
Tensor decomposition methods have recently proven to be efficient for compressing and accelerating neural networks. However, the problem of optimal decomposition structure determination is still not well studied while being quite important. Specifically, decomposition ranks present the crucial parameter controlling the compression-accuracy trade-off. In this paper, we introduce MARS -- a new efficient method for the automatic selection of ranks in general tensor decompositions. During training, the procedure learns binary masks over decomposition cores that "select" the optimal tensor structure. The learning is performed via relaxed maximum a posteriori (MAP) estimation in a specific Bayesian model. The proposed method achieves better results compared to previous works in various tasks.