ImageReFL: Balancing Quality and Diversity in Human-Aligned Diffusion Models

Recent advances in diffusion models have led to impressive image generation capabilities, but aligning these models with human preferences remains challenging. Reward-based fine-tuning using models trained on human feedback improves alignment but often harms diversity, producing less varied outputs. In this work, we address this trade-off with two contributions. First, we introduce \textit{combined generation}, a novel sampling strategy that applies a reward-tuned diffusion model only in the later stages of the generation process, while preserving the base model for earlier steps. This approach mitigates early-stage overfitting and helps retain global structure and diversity. Second, we propose \textit{ImageReFL}, a fine-tuning method that improves image diversity with minimal loss in quality by training on real images and incorporating multiple regularizers, including diffusion and ReFL losses. Our approach outperforms conventional reward tuning methods on standard quality and diversity metrics. A user study further confirms that our method better balances human preference alignment and visual diversity. The source code can be found at https://github.com/ControlGenAI/ImageReFL .

DreamBoothDPO: Improving Personalized Generation using Direct Preference Optimization

Personalized diffusion models have shown remarkable success in Text-to-Image (T2I) generation by enabling the injection of user-defined concepts into diverse contexts. However, balancing concept fidelity with contextual alignment remains a challenging open problem. In this work, we propose an RL-based approach that leverages the diverse outputs of T2I models to address this issue. Our method eliminates the need for human-annotated scores by generating a synthetic paired dataset for DPO-like training using external quality metrics. These better-worse pairs are specifically constructed to improve both concept fidelity and prompt adherence. Moreover, our approach supports flexible adjustment of the trade-off between image fidelity and textual alignment. Through multi-step training, our approach outperforms a naive baseline in convergence speed and output quality. We conduct extensive qualitative and quantitative analysis, demonstrating the effectiveness of our method across various architectures and fine-tuning techniques. The source code can be found at https://github.com/ControlGenAI/DreamBoothDPO.

Beyond Fine-Tuning: A Systematic Study of Sampling Techniques in Personalized Image Generation

Personalized text-to-image generation aims to create images tailored to user-defined concepts and textual descriptions. Balancing the fidelity of the learned concept with its ability for generation in various contexts presents a significant challenge. Existing methods often address this through diverse fine-tuning parameterizations and improved sampling strategies that integrate superclass trajectories during the diffusion process. While improved sampling offers a cost-effective, training-free solution for enhancing fine-tuned models, systematic analyses of these methods remain limited. Current approaches typically tie sampling strategies with fixed fine-tuning configurations, making it difficult to isolate their impact on generation outcomes. To address this issue, we systematically analyze sampling strategies beyond fine-tuning, exploring the impact of concept and superclass trajectories on the results. Building on this analysis, we propose a decision framework evaluating text alignment, computational constraints, and fidelity objectives to guide strategy selection. It integrates with diverse architectures and training approaches, systematically optimizing concept preservation, prompt adherence, and resource efficiency. The source code can be found at https://github.com/ControlGenAI/PersonGenSampler.

StyleDomain: Analysis of StyleSpace for Domain Adaptation of StyleGAN

Domain adaptation of GANs is a problem of fine-tuning the state-of-the-art GAN models (e.g. StyleGAN) pretrained on a large dataset to a specific domain with few samples (e.g. painting faces, sketches, etc.). While there are a great number of methods that tackle this problem in different ways there are still many important questions that remain unanswered. In this paper, we provide a systematic and in-depth analysis of the domain adaptation problem of GANs, focusing on the StyleGAN model. First, we perform a detailed exploration of the most important parts of StyleGAN that are responsible for adapting the generator to a new domain depending on the similarity between the source and target domains. In particular, we show that affine layers of StyleGAN can be sufficient for fine-tuning to similar domains. Second, inspired by these findings, we investigate StyleSpace to utilize it for domain adaptation. We show that there exist directions in the StyleSpace that can adapt StyleGAN to new domains. Further, we examine these directions and discover their many surprising properties. Finally, we leverage our analysis and findings to deliver practical improvements and applications in such standard tasks as image-to-image translation and cross-domain morphing.

Training Scale-Invariant Neural Networks on the Sphere Can Happen in Three Regimes

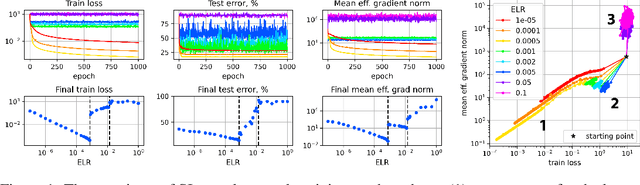
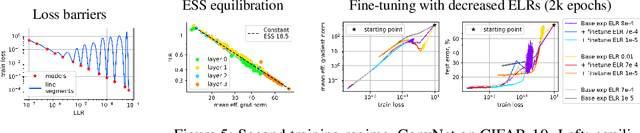
A fundamental property of deep learning normalization techniques, such as batch normalization, is making the pre-normalization parameters scale invariant. The intrinsic domain of such parameters is the unit sphere, and therefore their gradient optimization dynamics can be represented via spherical optimization with varying effective learning rate (ELR), which was studied previously. In this work, we investigate the properties of training scale-invariant neural networks directly on the sphere using a fixed ELR. We discover three regimes of such training depending on the ELR value: convergence, chaotic equilibrium, and divergence. We study these regimes in detail both on a theoretical examination of a toy example and on a thorough empirical analysis of real scale-invariant deep learning models. Each regime has unique features and reflects specific properties of the intrinsic loss landscape, some of which have strong parallels with previous research on both regular and scale-invariant neural networks training. Finally, we demonstrate how the discovered regimes are reflected in conventional training of normalized networks and how they can be leveraged to achieve better optima.