Probabilistic Intra-Retinal Layer Segmentation in 3-D OCT Images Using Global Shape Regularization

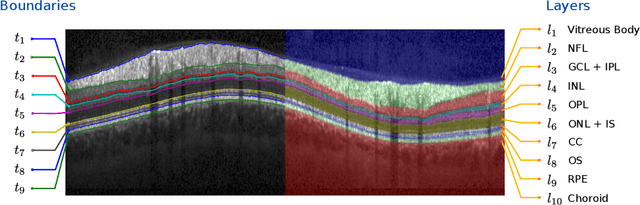
With the introduction of spectral-domain optical coherence tomography (OCT), resulting in a significant increase in acquisition speed, the fast and accurate segmentation of 3-D OCT scans has become evermore important. This paper presents a novel probabilistic approach, that models the appearance of retinal layers as well as the global shape variations of layer boundaries. Given an OCT scan, the full posterior distribution over segmentations is approximately inferred using a variational method enabling efficient probabilistic inference in terms of computationally tractable model components: Segmenting a full 3-D volume takes around a minute. Accurate segmentations demonstrate the benefit of using global shape regularization: We segmented 35 fovea-centered 3-D volumes with an average unsigned error of 2.46 $\pm$ 0.22 {\mu}m as well as 80 normal and 66 glaucomatous 2-D circular scans with errors of 2.92 $\pm$ 0.53 {\mu}m and 4.09 $\pm$ 0.98 {\mu}m respectively. Furthermore, we utilized the inferred posterior distribution to rate the quality of the segmentation, point out potentially erroneous regions and discriminate normal from pathological scans. No pre- or postprocessing was required and we used the same set of parameters for all data sets, underlining the robustness and out-of-the-box nature of our approach.

Efficient MRF Energy Minimization via Adaptive Diminishing Smoothing

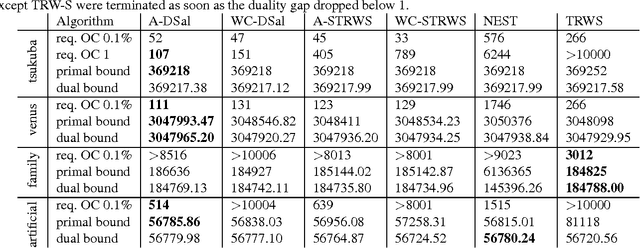
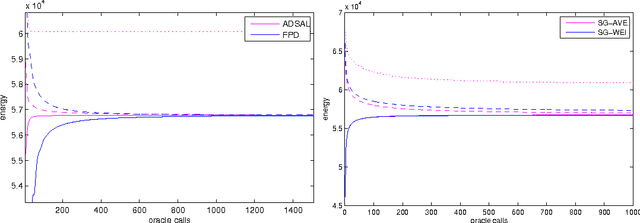
We consider the linear programming relaxation of an energy minimization problem for Markov Random Fields. The dual objective of this problem can be treated as a concave and unconstrained, but non-smooth function. The idea of smoothing the objective prior to optimization was recently proposed in a series of papers. Some of them suggested the idea to decrease the amount of smoothing (so called temperature) while getting closer to the optimum. However, no theoretical substantiation was provided. We propose an adaptive smoothing diminishing algorithm based on the duality gap between relaxed primal and dual objectives and demonstrate the efficiency of our approach with a smoothed version of Sequential Tree-Reweighted Message Passing (TRW-S) algorithm. The strategy is applicable to other algorithms as well, avoids adhoc tuning of the smoothing during iterations, and provably guarantees convergence to the optimum.

Getting Feasible Variable Estimates From Infeasible Ones: MRF Local Polytope Study

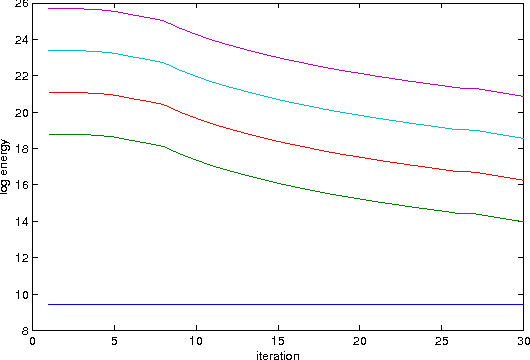
This paper proposes a method for construction of approximate feasible primal solutions from dual ones for large-scale optimization problems possessing certain separability properties. Whereas infeasible primal estimates can typically be produced from (sub-)gradients of the dual function, it is often not easy to project them to the primal feasible set, since the projection itself has a complexity comparable to the complexity of the initial problem. We propose an alternative efficient method to obtain feasibility and show that its properties influencing the convergence to the optimum are similar to the properties of the Euclidean projection. We apply our method to the local polytope relaxation of inference problems for Markov Random Fields and demonstrate its superiority over existing methods.