A First Derivative Potts Model for Segmentation and Denoising Using ILP
Paper and Code
Jan 10, 2018
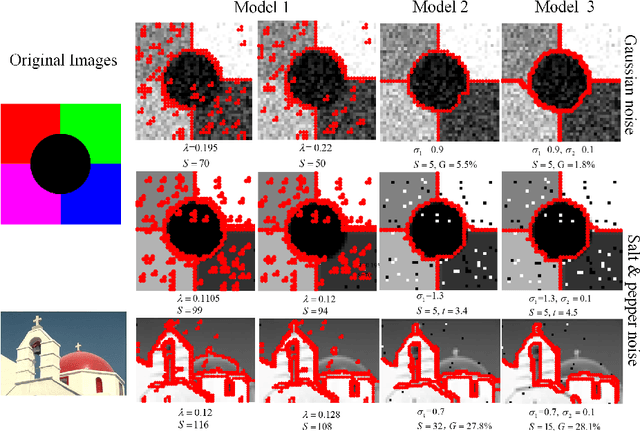
Unsupervised image segmentation and denoising are two fundamental tasks in image processing. Usually, graph based models such as multicut are used for segmentation and variational models are employed for denoising. Our approach addresses both problems at the same time. We propose a novel ILP formulation of the first derivative Potts model with the $\ell_1$ data term, where binary variables are introduced to deal with the $\ell_0$ norm of the regularization term. The ILP is then solved by a standard off-the-shelf MIP solver. Numerical experiments are compared with the multicut problem.
* 6 pages, 2 figures. To appear at Proceedings of International
Conference on Operations Research 2017, Berlin
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge