Symmetry-free SDP Relaxations for Affine Subspace Clustering

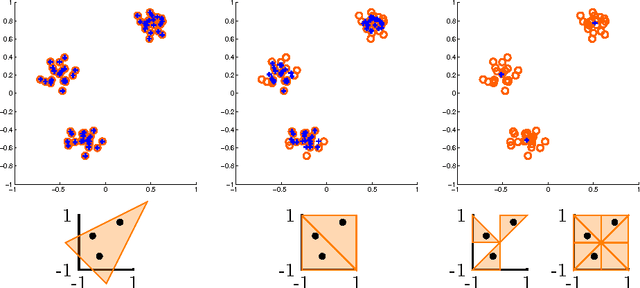
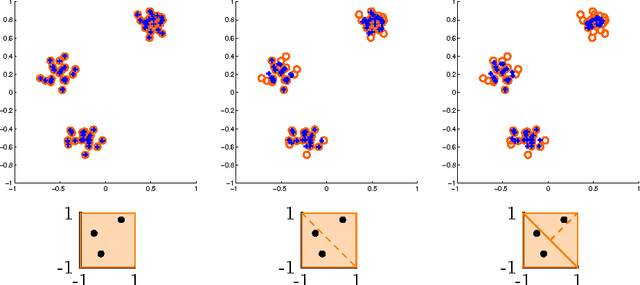
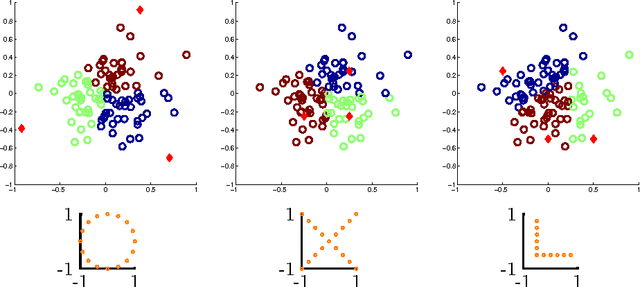
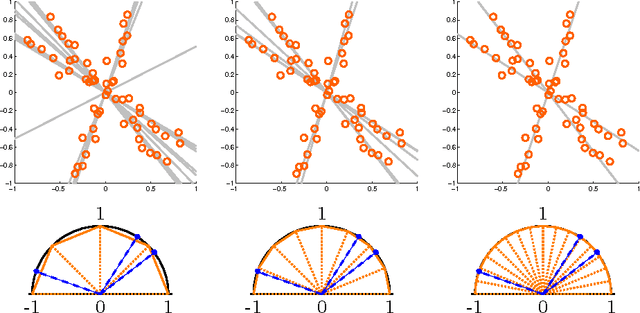
We consider clustering problems where the goal is to determine an optimal partition of a given point set in Euclidean space in terms of a collection of affine subspaces. While there is vast literature on heuristics for this kind of problem, such approaches are known to be susceptible to poor initializations and getting trapped in bad local optima. We alleviate these issues by introducing a semidefinite relaxation based on Lasserre's method of moments. While a similiar approach is known for classical Euclidean clustering problems, a generalization to our more general subspace scenario is not straightforward, due to the high symmetry of the objective function that weakens any convex relaxation. We therefore introduce a new mechanism for symmetry breaking based on covering the feasible region with polytopes. Additionally, we introduce and analyze a deterministic rounding heuristic.