On the Complexity of Inner Product Similarity Join
Paper and Code
Apr 07, 2016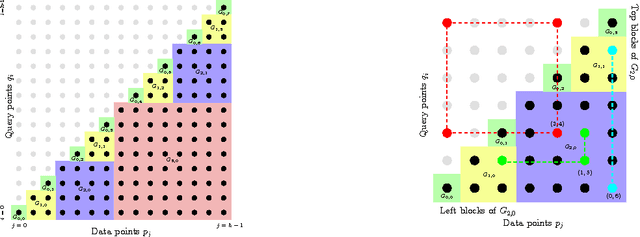
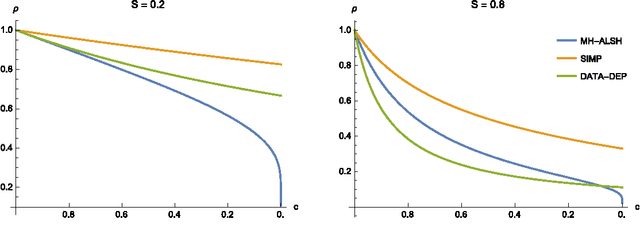
A number of tasks in classification, information retrieval, recommendation systems, and record linkage reduce to the core problem of inner product similarity join (IPS join): identifying pairs of vectors in a collection that have a sufficiently large inner product. IPS join is well understood when vectors are normalized and some approximation of inner products is allowed. However, the general case where vectors may have any length appears much more challenging. Recently, new upper bounds based on asymmetric locality-sensitive hashing (ALSH) and asymmetric embeddings have emerged, but little has been known on the lower bound side. In this paper we initiate a systematic study of inner product similarity join, showing new lower and upper bounds. Our main results are: * Approximation hardness of IPS join in subquadratic time, assuming the strong exponential time hypothesis. * New upper and lower bounds for (A)LSH-based algorithms. In particular, we show that asymmetry can be avoided by relaxing the LSH definition to only consider the collision probability of distinct elements. * A new indexing method for IPS based on linear sketches, implying that our hardness results are not far from being tight. Our technical contributions include new asymmetric embeddings that may be of independent interest. At the conceptual level we strive to provide greater clarity, for example by distinguishing among signed and unsigned variants of IPS join and shedding new light on the effect of asymmetry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge