Inductive Bias of Multi-Channel Linear Convolutional Networks with Bounded Weight Norm

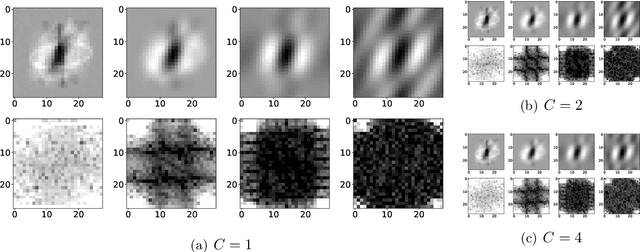
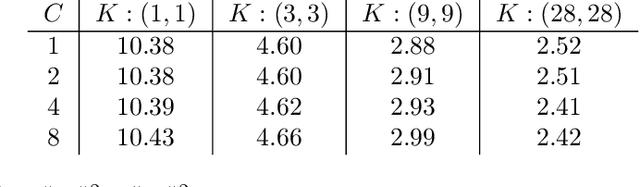
We study the function space characterization of the inductive bias resulting from controlling the $\ell_2$ norm of the weights in linear convolutional networks. We view this in terms of an induced regularizer in the function space given by the minimum norm of weights required to realize a linear function. For two layer linear convolutional networks with $C$ output channels and kernel size $K$, we show the following: (a) If the inputs to the network have a single channel, the induced regularizer for any $K$ is a norm given by a semidefinite program (SDP) that is independent of the number of output channels $C$. We further validate these results through a binary classification task on MNIST. (b) In contrast, for networks with multi-channel inputs, multiple output channels can be necessary to merely realize all matrix-valued linear functions and thus the inductive bias does depend on $C$. Further, for sufficiently large $C$, the induced regularizer for $K=1$ and $K=D$ are the nuclear norm and the $\ell_{2,1}$ group-sparse norm, respectively, of the Fourier coefficients -- both of which promote sparse structures.

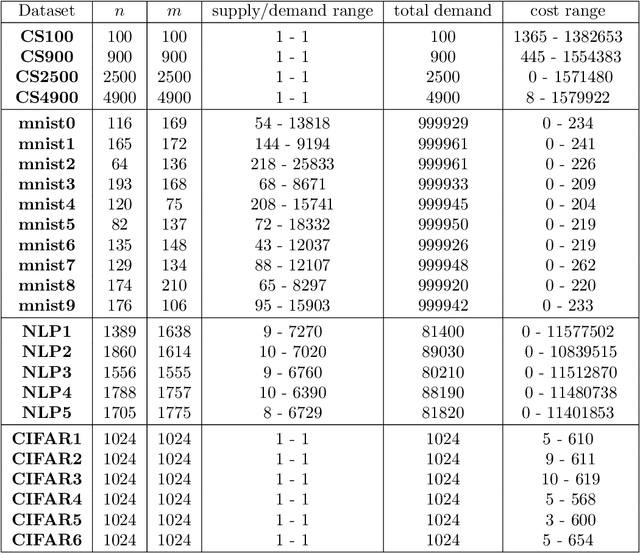
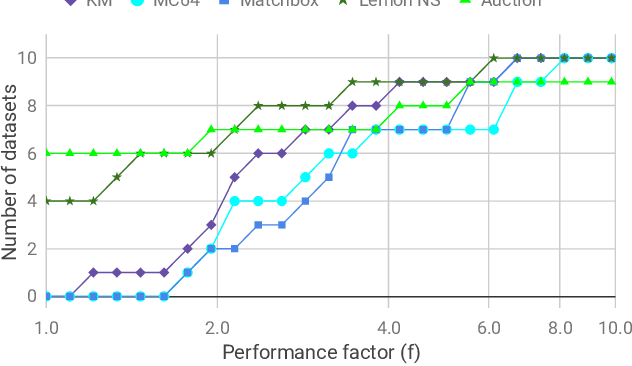
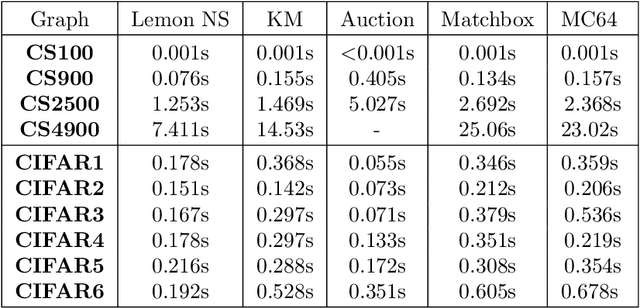
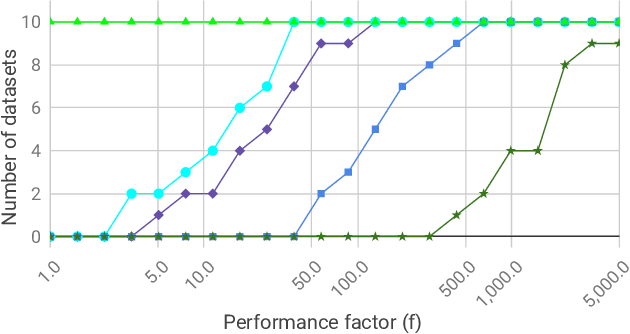
A Study of Performance of Optimal Transport

We investigate the problem of efficiently computing optimal transport (OT) distances, which is equivalent to the node-capacitated minimum cost maximum flow problem in a bipartite graph. We compare runtimes in computing OT distances on data from several domains, such as synthetic data of geometric shapes, embeddings of tokens in documents, and pixels in images. We show that in practice, combinatorial methods such as network simplex and augmenting path based algorithms can consistently outperform numerical matrix-scaling based methods such as Sinkhorn [Cuturi'13] and Greenkhorn [Altschuler et al'17], even in low accuracy regimes, with up to orders of magnitude speedups. Lastly, we present a new combinatorial algorithm that improves upon the classical Kuhn-Munkres algorithm.

Non-Adaptive Adaptive Sampling on Turnstile Streams

Adaptive sampling is a useful algorithmic tool for data summarization problems in the classical centralized setting, where the entire dataset is available to the single processor performing the computation. Adaptive sampling repeatedly selects rows of an underlying matrix $\mathbf{A}\in\mathbb{R}^{n\times d}$, where $n\gg d$, with probabilities proportional to their distances to the subspace of the previously selected rows. Intuitively, adaptive sampling seems to be limited to trivial multi-pass algorithms in the streaming model of computation due to its inherently sequential nature of assigning sampling probabilities to each row only after the previous iteration is completed. Surprisingly, we show this is not the case by giving the first one-pass algorithms for adaptive sampling on turnstile streams and using space $\text{poly}(d,k,\log n)$, where $k$ is the number of adaptive sampling rounds to be performed. Our adaptive sampling procedure has a number of applications to various data summarization problems that either improve state-of-the-art or have only been previously studied in the more relaxed row-arrival model. We give the first relative-error algorithms for column subset selection, subspace approximation, projective clustering, and volume maximization on turnstile streams that use space sublinear in $n$. We complement our volume maximization algorithmic results with lower bounds that are tight up to lower order terms, even for multi-pass algorithms. By a similar construction, we also obtain lower bounds for volume maximization in the row-arrival model, which we match with competitive upper bounds. See paper for full abstract.

Scaling up Kernel Ridge Regression via Locality Sensitive Hashing

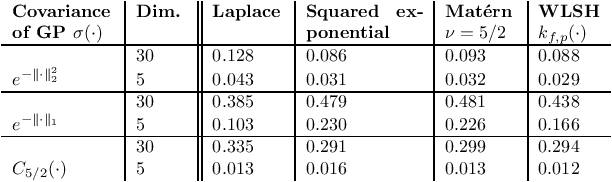
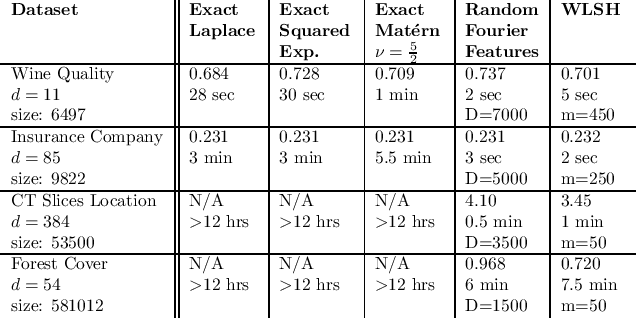
Random binning features, introduced in the seminal paper of Rahimi and Recht (2007), are an efficient method for approximating a kernel matrix using locality sensitive hashing. Random binning features provide a very simple and efficient way of approximating the Laplace kernel but unfortunately do not apply to many important classes of kernels, notably ones that generate smooth Gaussian processes, such as the Gaussian kernel and Matern kernel. In this paper, we introduce a simple weighted version of random binning features and show that the corresponding kernel function generates Gaussian processes of any desired smoothness. We show that our weighted random binning features provide a spectral approximation to the corresponding kernel matrix, leading to efficient algorithms for kernel ridge regression. Experiments on large scale regression datasets show that our method outperforms the accuracy of random Fourier features method.

Randomized Smoothing of All Shapes and Sizes

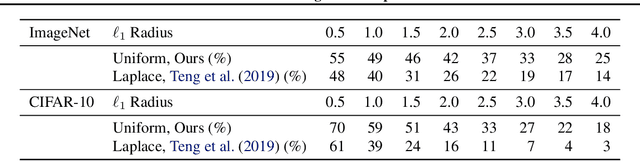
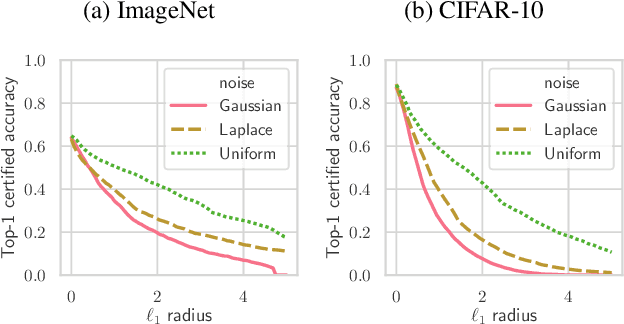
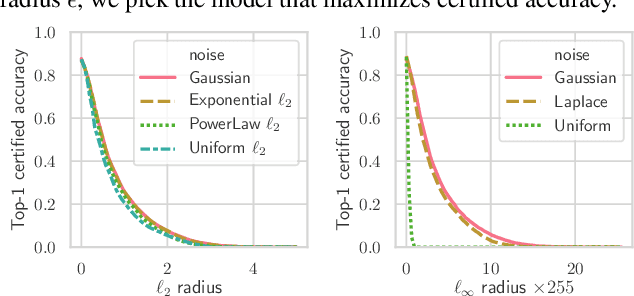
Randomized smoothing is a recently proposed defense against adversarial attacks that has achieved state-of-the-art provable robustness against $\ell_2$ perturbations. Soon after, a number of works devised new randomized smoothing schemes for other metrics, such as $\ell_1$ or $\ell_\infty$; however, for each geometry, substantial effort was needed to derive new robustness guarantees. This begs the question: can we find a general theory for randomized smoothing? In this work we propose a novel framework for devising and analyzing randomized smoothing schemes, and validate its effectiveness in practice. Our theoretical contributions are as follows: (1) We show that for an appropriate notion of "optimal", the optimal smoothing distributions for any "nice" norm have level sets given by the *Wulff Crystal* of that norm. (2) We propose two novel and complementary methods for deriving provably robust radii for any smoothing distribution. Finally, (3) we show fundamental limits to current randomized smoothing techniques via the theory of *Banach space cotypes*. By combining (1) and (2), we significantly improve the state-of-the-art certified accuracy in $\ell_1$ on standard datasets. On the other hand, using (3), we show that, without more information than label statistics under random input perturbations, randomized smoothing cannot achieve nontrivial certified accuracy against perturbations of $\ell_p$-norm $\Omega(\min(1, d^{\frac{1}{p}-\frac{1}{2}}))$, when the input dimension $d$ is large. We provide code in github.com/tonyduan/rs4a.

Provably Robust Deep Learning via Adversarially Trained Smoothed Classifiers

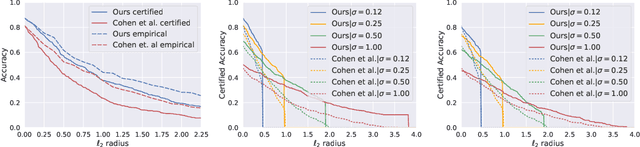
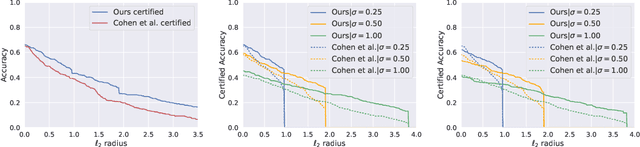
Recent works have shown the effectiveness of randomized smoothing as a scalable technique for building neural network-based classifiers that are provably robust to $\ell_2$-norm adversarial perturbations. In this paper, we employ adversarial training to improve the performance of randomized smoothing. We design an adapted attack for smoothed classifiers, and we show how this attack can be used in an adversarial training setting to boost the provable robustness of smoothed classifiers. We demonstrate through extensive experimentation that our method consistently outperforms all existing provably $\ell_2$-robust classifiers by a significant margin on ImageNet and CIFAR-10, establishing the state-of-the-art for provable $\ell_2$-defenses. Our code and trained models are available at http://github.com/Hadisalman/smoothing-adversarial .

SANNS: Scaling Up Secure Approximate k-Nearest Neighbors Search

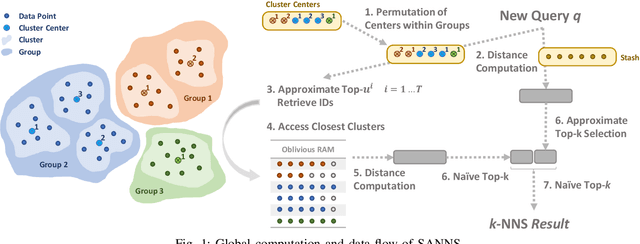
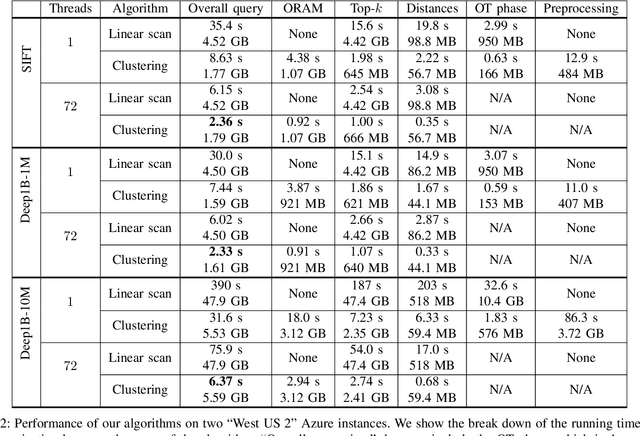
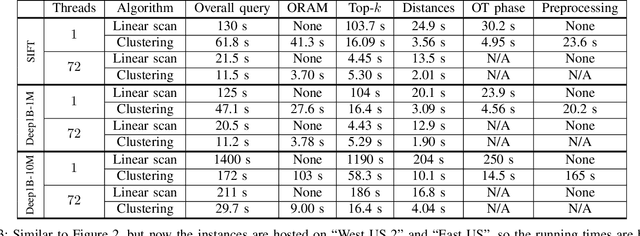
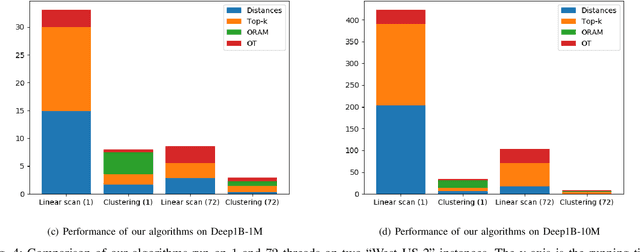
We present new secure protocols for approximate $k$-nearest neighbor search ($k$-NNS) over the Euclidean distance in the semi-honest model. Our implementation is able to handle massive datasets efficiently. On the algorithmic front, we show a new circuit for the approximate top-$k$ selection from $n$ numbers that is built from merely $O(n + \mathrm{poly}(k))$ comparators. Using this circuit as a subroutine, we design new approximate $k$-NNS algorithms and two corresponding secure protocols: 1) optimized linear scan; 2) clustering-based sublinear time algorithm. Our secure protocols utilize a combination of additively-homomorphic encryption, garbled circuit and Oblivious RAM. Along the way, we introduce various optimizations to these primitives, which drastically improve concrete efficiency. We evaluate the new protocols empirically and show that they are able to handle datasets that are significantly larger than in the prior work. For instance, running on two standard Azure instances within the same availability zone, for a dataset of $96$-dimensional descriptors of $10\,000\,000$ images, we can find $10$ nearest neighbors with average accuracy $0.9$ in under $10$ seconds improving upon prior work by at least two orders of magnitude.

Learning Sublinear-Time Indexing for Nearest Neighbor Search

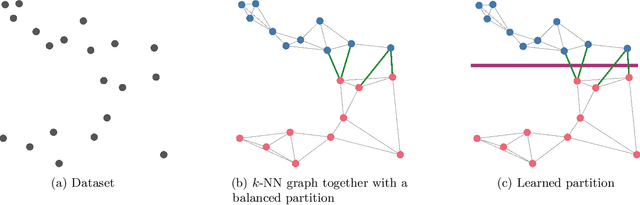
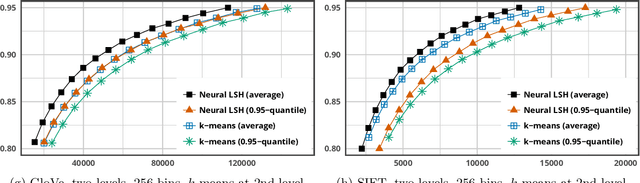
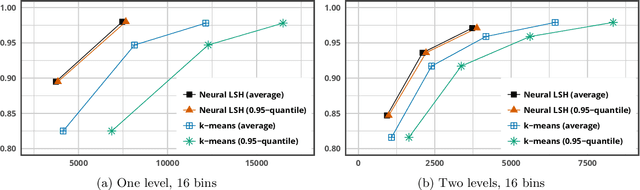
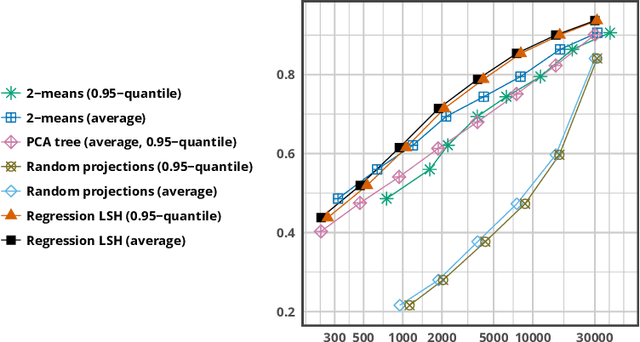
Most of the efficient sublinear-time indexing algorithms for the high-dimensional nearest neighbor search problem (NNS) are based on space partitions of the ambient space $\mathbb{R}^d$. Inspired by recent theoretical work on NNS for general metric spaces [Andoni, Naor, Nikolov, Razenshteyn, Waingarten STOC 2018, FOCS 2018], we develop a new framework for constructing such partitions that reduces the problem to balanced graph partitioning followed by supervised classification. We instantiate this general approach with the KaHIP graph partitioner [Sanders, Schulz SEA 2013] and neural networks, respectively, to obtain a new partitioning procedure called Neural Locality-Sensitive Hashing (Neural LSH). On several standard benchmarks for NNS, our experiments show that the partitions found by Neural LSH consistently outperform partitions found by quantization- and tree-based methods.

Adversarial Examples from Cryptographic Pseudo-Random Generators

In our recent work (Bubeck, Price, Razenshteyn, arXiv:1805.10204) we argued that adversarial examples in machine learning might be due to an inherent computational hardness of the problem. More precisely, we constructed a binary classification task for which (i) a robust classifier exists; yet no non-trivial accuracy can be obtained with an efficient algorithm in (ii) the statistical query model. In the present paper we significantly strengthen both (i) and (ii): we now construct a task which admits (i') a maximally robust classifier (that is it can tolerate perturbations of size comparable to the size of the examples themselves); and moreover we prove computational hardness of learning this task under (ii') a standard cryptographic assumption.

Nonlinear Dimension Reduction via Outer Bi-Lipschitz Extensions

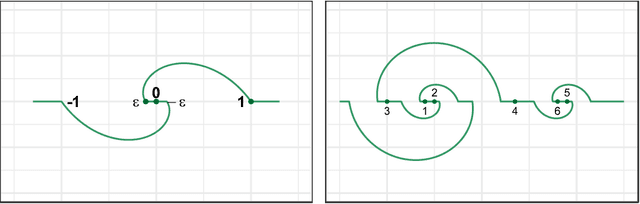
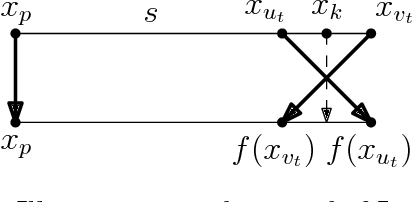
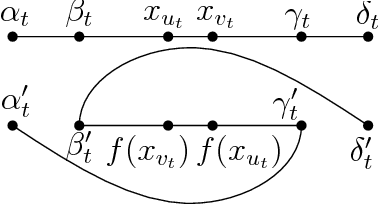
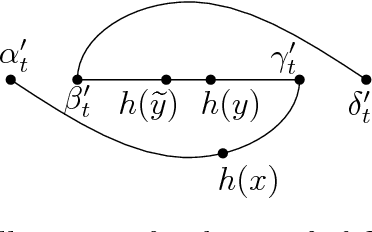
We introduce and study the notion of an outer bi-Lipschitz extension of a map between Euclidean spaces. The notion is a natural analogue of the notion of a Lipschitz extension of a Lipschitz map. We show that for every map $f$ there exists an outer bi-Lipschitz extension $f'$ whose distortion is greater than that of $f$ by at most a constant factor. This result can be seen as a counterpart of the classic Kirszbraun theorem for outer bi-Lipschitz extensions. We also study outer bi-Lipschitz extensions of near-isometric maps and show upper and lower bounds for them. Then, we present applications of our results to prioritized and terminal dimension reduction problems. * We prove a prioritized variant of the Johnson-Lindenstrauss lemma: given a set of points $X\subset \mathbb{R}^d$ of size $N$ and a permutation ("priority ranking") of $X$, there exists an embedding $f$ of $X$ into $\mathbb{R}^{O(\log N)}$ with distortion $O(\log \log N)$ such that the point of rank $j$ has only $O(\log^{3 + \varepsilon} j)$ non-zero coordinates - more specifically, all but the first $O(\log^{3+\varepsilon} j)$ coordinates are equal to $0$; the distortion of $f$ restricted to the first $j$ points (according to the ranking) is at most $O(\log\log j)$. The result makes a progress towards answering an open question by Elkin, Filtser, and Neiman about prioritized dimension reductions. * We prove that given a set $X$ of $N$ points in $\mathbb{R}^d$, there exists a terminal dimension reduction embedding of $\mathbb{R}^d$ into $\mathbb{R}^{d'}$, where $d' = O\left(\frac{\log N}{\varepsilon^4}\right)$, which preserves distances $\|x-y\|$ between points $x\in X$ and $y \in \mathbb{R}^{d}$, up to a multiplicative factor of $1 \pm \varepsilon$. This improves a recent result by Elkin, Filtser, and Neiman. The dimension reductions that we obtain are nonlinear, and this nonlinearity is necessary.