Learning Sublinear-Time Indexing for Nearest Neighbor Search

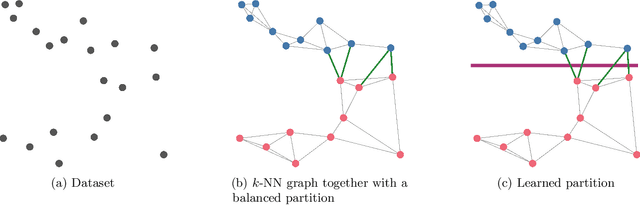
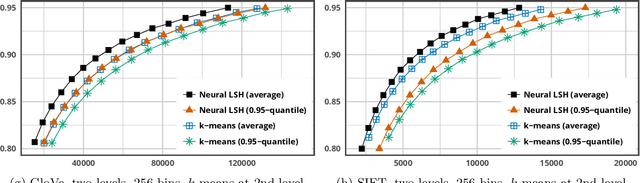
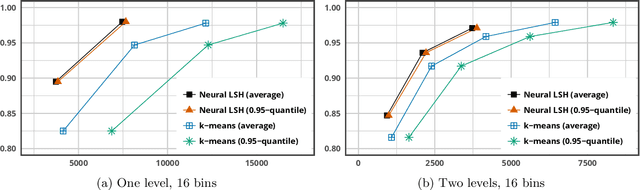
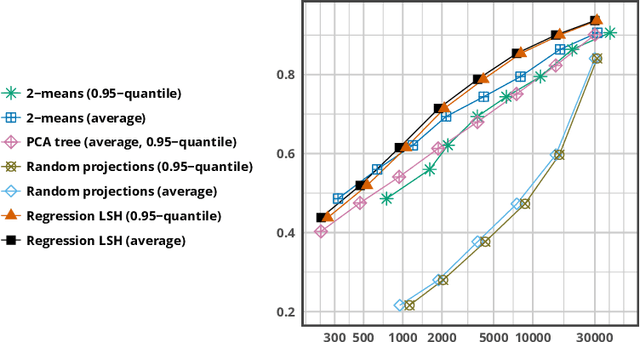
Most of the efficient sublinear-time indexing algorithms for the high-dimensional nearest neighbor search problem (NNS) are based on space partitions of the ambient space $\mathbb{R}^d$. Inspired by recent theoretical work on NNS for general metric spaces [Andoni, Naor, Nikolov, Razenshteyn, Waingarten STOC 2018, FOCS 2018], we develop a new framework for constructing such partitions that reduces the problem to balanced graph partitioning followed by supervised classification. We instantiate this general approach with the KaHIP graph partitioner [Sanders, Schulz SEA 2013] and neural networks, respectively, to obtain a new partitioning procedure called Neural Locality-Sensitive Hashing (Neural LSH). On several standard benchmarks for NNS, our experiments show that the partitions found by Neural LSH consistently outperform partitions found by quantization- and tree-based methods.