BalanceKV: KV Cache Compression through Discrepancy Theory

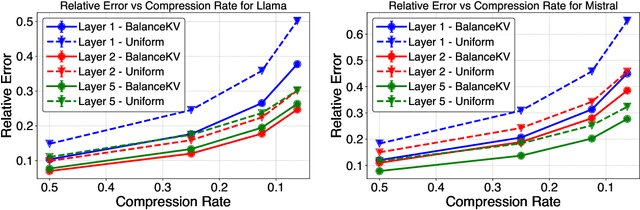
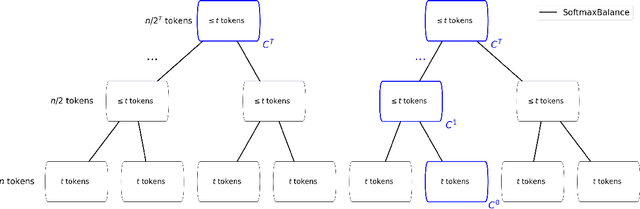
Large language models (LLMs) have achieved impressive success, but their high memory requirements present challenges for long-context token generation. The memory complexity of long-context LLMs is primarily due to the need to store Key-Value (KV) embeddings in their KV cache. We present BalanceKV, a KV cache compression method based on geometric sampling process stemming from Banaszczyk's vector balancing theory, which introduces dependencies informed by the geometry of keys and value tokens, and improves precision. BalanceKV offers both theoretically proven and empirically validated performance improvements over existing methods.

PolarQuant: Quantizing KV Caches with Polar Transformation

Large language models (LLMs) require significant memory to store Key-Value (KV) embeddings in their KV cache, especially when handling long-range contexts. Quantization of these KV embeddings is a common technique to reduce memory consumption. This work introduces PolarQuant, a novel quantization method employing random preconditioning and polar transformation. Our method transforms the KV embeddings into polar coordinates using an efficient recursive algorithm and then quantizes resulting angles. Our key insight is that, after random preconditioning, the angles in the polar representation exhibit a tightly bounded and highly concentrated distribution with an analytically computable form. This nice distribution eliminates the need for explicit normalization, a step required by traditional quantization methods which introduces significant memory overhead because quantization parameters (e.g., zero point and scale) must be stored in full precision per each data block. PolarQuant bypasses this normalization step, enabling substantial memory savings. The long-context evaluation demonstrates that PolarQuant compresses the KV cache by over x4.2 while achieving the best quality scores compared to the state-of-the-art methods.

QJL: 1-Bit Quantized JL Transform for KV Cache Quantization with Zero Overhead

Serving LLMs requires substantial memory due to the storage requirements of Key-Value (KV) embeddings in the KV cache, which grows with sequence length. An effective approach to compress KV cache is quantization. However, traditional quantization methods face significant memory overhead due to the need to store quantization constants (at least a zero point and a scale) in full precision per data block. Depending on the block size, this overhead can add 1 or 2 bits per quantized number. We introduce QJL, a new quantization approach that consists of a Johnson-Lindenstrauss (JL) transform followed by sign-bit quantization. In contrast to existing methods, QJL eliminates memory overheads by removing the need for storing quantization constants. We propose an asymmetric estimator for the inner product of two vectors and demonstrate that applying QJL to one vector and a standard JL transform without quantization to the other provides an unbiased estimator with minimal distortion. We have developed an efficient implementation of the QJL sketch and its corresponding inner product estimator, incorporating a lightweight CUDA kernel for optimized computation. When applied across various LLMs and NLP tasks to quantize the KV cache to only 3 bits, QJL demonstrates a more than fivefold reduction in KV cache memory usage without compromising accuracy, all while achieving faster runtime. Codes are available at \url{https://github.com/amirzandieh/QJL}.

SubGen: Token Generation in Sublinear Time and Memory

Despite the significant success of large language models (LLMs), their extensive memory requirements pose challenges for deploying them in long-context token generation. The substantial memory footprint of LLM decoders arises from the necessity to store all previous tokens in the attention module, a requirement imposed by key-value (KV) caching. In this work, our focus is on developing an efficient compression technique for the KV cache. Empirical evidence indicates a significant clustering tendency within key embeddings in the attention module. Building on this key insight, we have devised a novel caching method with sublinear complexity, employing online clustering on key tokens and online $\ell_2$ sampling on values. The result is a provably accurate and efficient attention decoding algorithm, termed SubGen. Not only does this algorithm ensure a sublinear memory footprint and sublinear time complexity, but we also establish a tight error bound for our approach. Empirical evaluations on long-context question-answering tasks demonstrate that SubGen significantly outperforms existing and state-of-the-art KV cache compression methods in terms of performance and efficiency.

HyperAttention: Long-context Attention in Near-Linear Time

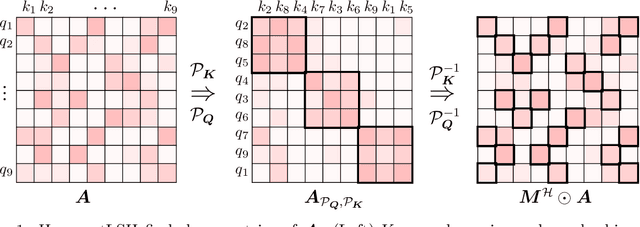
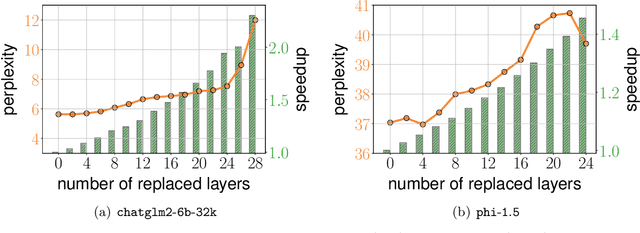
We present an approximate attention mechanism named HyperAttention to address the computational challenges posed by the growing complexity of long contexts used in Large Language Models (LLMs). Recent work suggests that in the worst-case scenario, quadratic time is necessary unless the entries of the attention matrix are bounded or the matrix has low stable rank. We introduce two parameters which measure: (1) the max column norm in the normalized attention matrix, and (2) the ratio of row norms in the unnormalized attention matrix after detecting and removing large entries. We use these fine-grained parameters to capture the hardness of the problem. Despite previous lower bounds, we are able to achieve a linear time sampling algorithm even when the matrix has unbounded entries or a large stable rank, provided the above parameters are small. HyperAttention features a modular design that easily accommodates integration of other fast low-level implementations, particularly FlashAttention. Empirically, employing Locality Sensitive Hashing (LSH) to identify large entries, HyperAttention outperforms existing methods, giving significant speed improvements compared to state-of-the-art solutions like FlashAttention. We validate the empirical performance of HyperAttention on a variety of different long-context length datasets. For example, HyperAttention makes the inference time of ChatGLM2 50\% faster on 32k context length while perplexity increases from 5.6 to 6.3. On larger context length, e.g., 131k, with causal masking, HyperAttention offers 5-fold speedup on a single attention layer.

KDEformer: Accelerating Transformers via Kernel Density Estimation

Dot-product attention mechanism plays a crucial role in modern deep architectures (e.g., Transformer) for sequence modeling, however, na\"ive exact computation of this model incurs quadratic time and memory complexities in sequence length, hindering the training of long-sequence models. Critical bottlenecks are due to the computation of partition functions in the denominator of softmax function as well as the multiplication of the softmax matrix with the matrix of values. Our key observation is that the former can be reduced to a variant of the kernel density estimation (KDE) problem, and an efficient KDE solver can be further utilized to accelerate the latter via subsampling-based fast matrix products. Our proposed KDEformer can approximate the attention in sub-quadratic time with provable spectral norm bounds, while all prior results merely provide entry-wise error bounds. Empirically, we verify that KDEformer outperforms other attention approximations in terms of accuracy, memory, and runtime on various pre-trained models. On BigGAN image generation, we achieve better generative scores than the exact computation with over $4\times$ speedup. For ImageNet classification with T2T-ViT, KDEformer shows over $18\times$ speedup while the accuracy drop is less than $0.5\%$.

Fast Neural Kernel Embeddings for General Activations

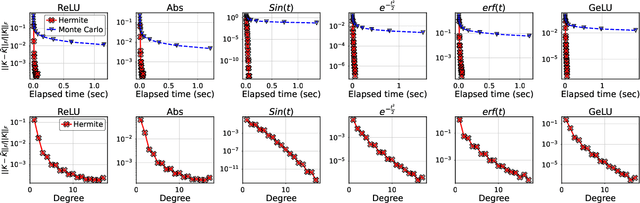
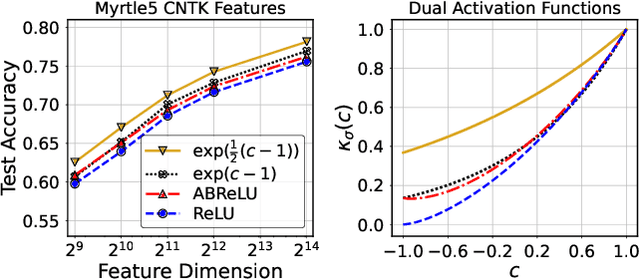
Infinite width limit has shed light on generalization and optimization aspects of deep learning by establishing connections between neural networks and kernel methods. Despite their importance, the utility of these kernel methods was limited in large-scale learning settings due to their (super-)quadratic runtime and memory complexities. Moreover, most prior works on neural kernels have focused on the ReLU activation, mainly due to its popularity but also due to the difficulty of computing such kernels for general activations. In this work, we overcome such difficulties by providing methods to work with general activations. First, we compile and expand the list of activation functions admitting exact dual activation expressions to compute neural kernels. When the exact computation is unknown, we present methods to effectively approximate them. We propose a fast sketching method that approximates any multi-layered Neural Network Gaussian Process (NNGP) kernel and Neural Tangent Kernel (NTK) matrices for a wide range of activation functions, going beyond the commonly analyzed ReLU activation. This is done by showing how to approximate the neural kernels using the truncated Hermite expansion of any desired activation functions. While most prior works require data points on the unit sphere, our methods do not suffer from such limitations and are applicable to any dataset of points in $\mathbb{R}^d$. Furthermore, we provide a subspace embedding for NNGP and NTK matrices with near input-sparsity runtime and near-optimal target dimension which applies to any \emph{homogeneous} dual activation functions with rapidly convergent Taylor expansion. Empirically, with respect to exact convolutional NTK (CNTK) computation, our method achieves $106\times$ speedup for approximate CNTK of a 5-layer Myrtle network on CIFAR-10 dataset.

Near Optimal Reconstruction of Spherical Harmonic Expansions

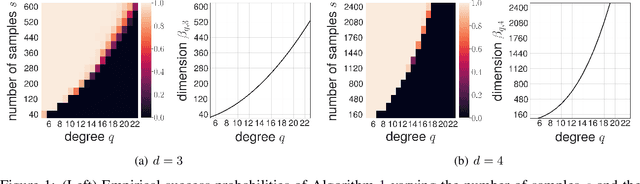
We propose an algorithm for robust recovery of the spherical harmonic expansion of functions defined on the d-dimensional unit sphere $\mathbb{S}^{d-1}$ using a near-optimal number of function evaluations. We show that for any $f \in L^2(\mathbb{S}^{d-1})$, the number of evaluations of $f$ needed to recover its degree-$q$ spherical harmonic expansion equals the dimension of the space of spherical harmonics of degree at most $q$ up to a logarithmic factor. Moreover, we develop a simple yet efficient algorithm to recover degree-$q$ expansion of $f$ by only evaluating the function on uniformly sampled points on $\mathbb{S}^{d-1}$. Our algorithm is based on the connections between spherical harmonics and Gegenbauer polynomials and leverage score sampling methods. Unlike the prior results on fast spherical harmonic transform, our proposed algorithm works efficiently using a nearly optimal number of samples in any dimension d. We further illustrate the empirical performance of our algorithm on numerical examples.

Leverage Score Sampling for Tensor Product Matrices in Input Sparsity Time

We give an input sparsity time sampling algorithm for spectrally approximating the Gram matrix corresponding to the $q$-fold column-wise tensor product of $q$ matrices using a nearly optimal number of samples, improving upon all previously known methods by poly$(q)$ factors. Furthermore, for the important special care of the $q$-fold self-tensoring of a dataset, which is the feature matrix of the degree-$q$ polynomial kernel, the leading term of our method's runtime is proportional to the size of the dataset and has no dependence on $q$. Previous techniques either incur a poly$(q)$ factor slowdown in their runtime or remove the dependence on $q$ at the expense of having sub-optimal target dimension, and depend quadratically on the number of data-points in their runtime. Our sampling technique relies on a collection of $q$ partially correlated random projections which can be simultaneously applied to a dataset $X$ in total time that only depends on the size of $X$, and at the same time their $q$-fold Kronecker product acts as a near-isometry for any fixed vector in the column span of $X^{\otimes q}$. We show that our sampling methods generalize to other classes of kernels beyond polynomial, such as Gaussian and Neural Tangent kernels.

Random Gegenbauer Features for Scalable Kernel Methods

We propose efficient random features for approximating a new and rich class of kernel functions that we refer to as Generalized Zonal Kernels (GZK). Our proposed GZK family, generalizes the zonal kernels (i.e., dot-product kernels on the unit sphere) by introducing radial factors in their Gegenbauer series expansion, and includes a wide range of ubiquitous kernel functions such as the entirety of dot-product kernels as well as the Gaussian and the recently introduced Neural Tangent kernels. Interestingly, by exploiting the reproducing property of the Gegenbauer polynomials, we can construct efficient random features for the GZK family based on randomly oriented Gegenbauer kernels. We prove subspace embedding guarantees for our Gegenbauer features which ensures that our features can be used for approximately solving learning problems such as kernel k-means clustering, kernel ridge regression, etc. Empirical results show that our proposed features outperform recent kernel approximation methods.