BalanceKV: KV Cache Compression through Discrepancy Theory

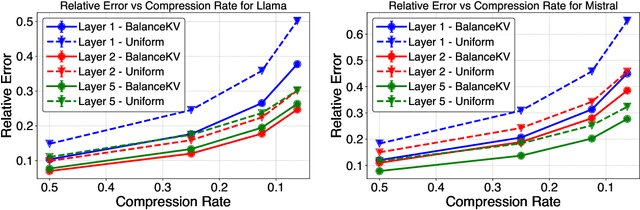
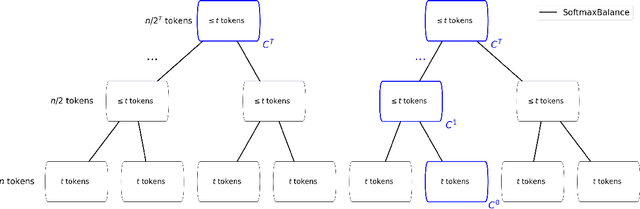
Large language models (LLMs) have achieved impressive success, but their high memory requirements present challenges for long-context token generation. The memory complexity of long-context LLMs is primarily due to the need to store Key-Value (KV) embeddings in their KV cache. We present BalanceKV, a KV cache compression method based on geometric sampling process stemming from Banaszczyk's vector balancing theory, which introduces dependencies informed by the geometry of keys and value tokens, and improves precision. BalanceKV offers both theoretically proven and empirically validated performance improvements over existing methods.

On the Robustness of Spectral Algorithms for Semirandom Stochastic Block Models

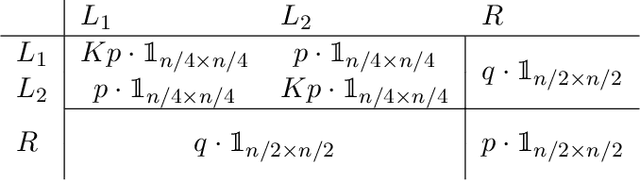
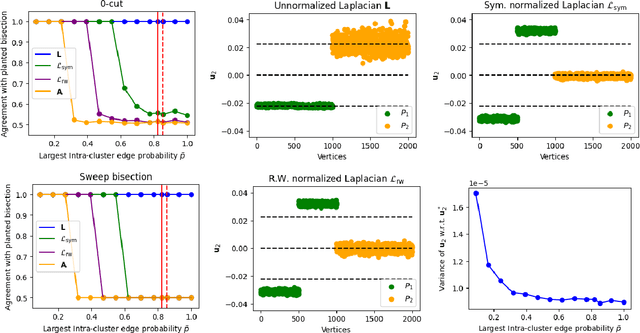
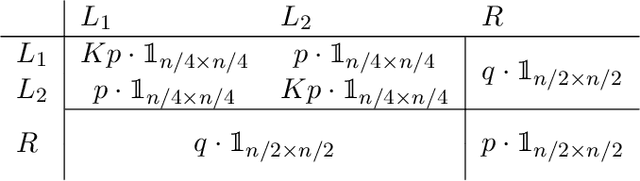
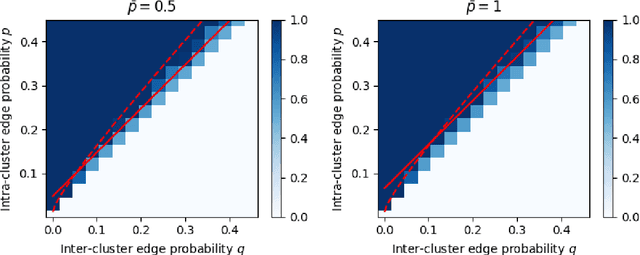
In a graph bisection problem, we are given a graph $G$ with two equally-sized unlabeled communities, and the goal is to recover the vertices in these communities. A popular heuristic, known as spectral clustering, is to output an estimated community assignment based on the eigenvector corresponding to the second smallest eigenvalue of the Laplacian of $G$. Spectral algorithms can be shown to provably recover the cluster structure for graphs generated from certain probabilistic models, such as the Stochastic Block Model (SBM). However, spectral clustering is known to be non-robust to model mis-specification. Techniques based on semidefinite programming have been shown to be more robust, but they incur significant computational overheads. In this work, we study the robustness of spectral algorithms against semirandom adversaries. Informally, a semirandom adversary is allowed to ``helpfully'' change the specification of the model in a way that is consistent with the ground-truth solution. Our semirandom adversaries in particular are allowed to add edges inside clusters or increase the probability that an edge appears inside a cluster. Semirandom adversaries are a useful tool to determine the extent to which an algorithm has overfit to statistical assumptions on the input. On the positive side, we identify classes of semirandom adversaries under which spectral bisection using the _unnormalized_ Laplacian is strongly consistent, i.e., it exactly recovers the planted partitioning. On the negative side, we show that in these classes spectral bisection with the _normalized_ Laplacian outputs a partitioning that makes a classification mistake on a constant fraction of the vertices. Finally, we demonstrate numerical experiments that complement our theoretical findings.

Efficient and Local Parallel Random Walks

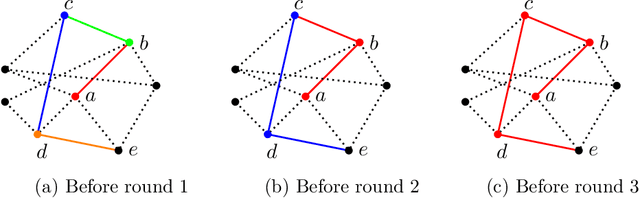
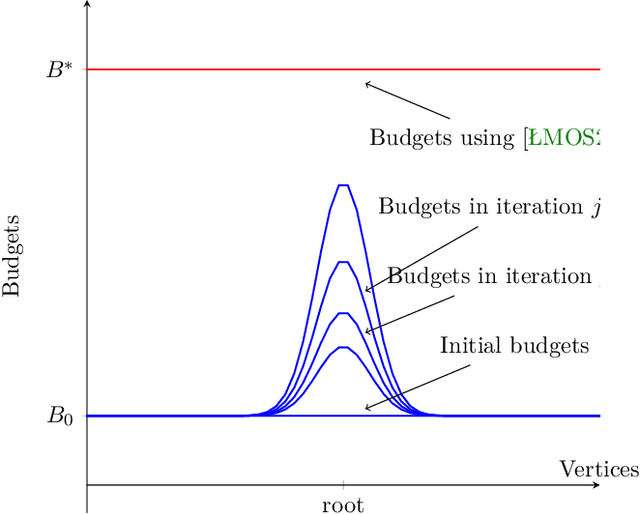
Random walks are a fundamental primitive used in many machine learning algorithms with several applications in clustering and semi-supervised learning. Despite their relevance, the first efficient parallel algorithm to compute random walks has been introduced very recently (Lacki et al.). Unfortunately their method has a fundamental shortcoming: their algorithm is non-local in that it heavily relies on computing random walks out of all nodes in the input graph, even though in many practical applications one is interested in computing random walks only from a small subset of nodes in the graph. In this paper, we present a new algorithm that overcomes this limitation by building random walk efficiently and locally at the same time. We show that our technique is both memory and round efficient, and in particular yields an efficient parallel local clustering algorithm. Finally, we complement our theoretical analysis with experimental results showing that our algorithm is significantly more scalable than previous approaches.

Scaling up Kernel Ridge Regression via Locality Sensitive Hashing

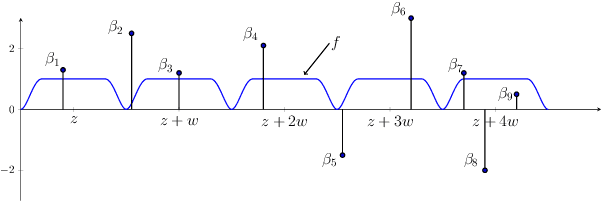
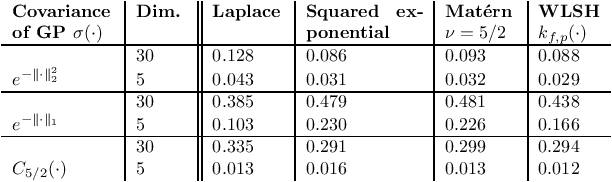
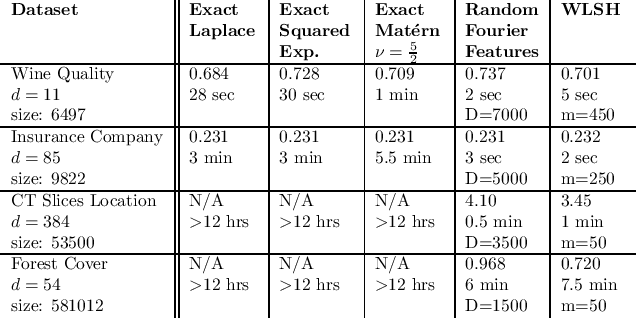
Random binning features, introduced in the seminal paper of Rahimi and Recht (2007), are an efficient method for approximating a kernel matrix using locality sensitive hashing. Random binning features provide a very simple and efficient way of approximating the Laplace kernel but unfortunately do not apply to many important classes of kernels, notably ones that generate smooth Gaussian processes, such as the Gaussian kernel and Matern kernel. In this paper, we introduce a simple weighted version of random binning features and show that the corresponding kernel function generates Gaussian processes of any desired smoothness. We show that our weighted random binning features provide a spectral approximation to the corresponding kernel matrix, leading to efficient algorithms for kernel ridge regression. Experiments on large scale regression datasets show that our method outperforms the accuracy of random Fourier features method.

A Universal Sampling Method for Reconstructing Signals with Simple Fourier Transforms

Reconstructing continuous signals from a small number of discrete samples is a fundamental problem across science and engineering. In practice, we are often interested in signals with 'simple' Fourier structure, such as bandlimited, multiband, and Fourier sparse signals. More broadly, any prior knowledge about a signal's Fourier power spectrum can constrain its complexity. Intuitively, signals with more highly constrained Fourier structure require fewer samples to reconstruct. We formalize this intuition by showing that, roughly, a continuous signal from a given class can be approximately reconstructed using a number of samples proportional to the *statistical dimension* of the allowed power spectrum of that class. Further, in nearly all settings, this natural measure tightly characterizes the sample complexity of signal reconstruction. Surprisingly, we also show that, up to logarithmic factors, a universal non-uniform sampling strategy can achieve this optimal complexity for *any class of signals*. We present a simple and efficient algorithm for recovering a signal from the samples taken. For bandlimited and sparse signals, our method matches the state-of-the-art. At the same time, it gives the first computationally and sample efficient solution to a broad range of problems, including multiband signal reconstruction and kriging and Gaussian process regression tasks in one dimension. Our work is based on a novel connection between randomized linear algebra and signal reconstruction with constrained Fourier structure. We extend tools based on statistical leverage score sampling and column-based matrix reconstruction to the approximation of continuous linear operators that arise in signal reconstruction. We believe that these extensions are of independent interest and serve as a foundation for tackling a broad range of continuous time problems using randomized methods.

Random Fourier Features for Kernel Ridge Regression: Approximation Bounds and Statistical Guarantees

Random Fourier features is one of the most popular techniques for scaling up kernel methods, such as kernel ridge regression. However, despite impressive empirical results, the statistical properties of random Fourier features are still not well understood. In this paper we take steps toward filling this gap. Specifically, we approach random Fourier features from a spectral matrix approximation point of view, give tight bounds on the number of Fourier features required to achieve a spectral approximation, and show how spectral matrix approximation bounds imply statistical guarantees for kernel ridge regression. Qualitatively, our results are twofold: on the one hand, we show that random Fourier feature approximation can provably speed up kernel ridge regression under reasonable assumptions. At the same time, we show that the method is suboptimal, and sampling from a modified distribution in Fourier space, given by the leverage function of the kernel, yields provably better performance. We study this optimal sampling distribution for the Gaussian kernel, achieving a nearly complete characterization for the case of low-dimensional bounded datasets. Based on this characterization, we propose an efficient sampling scheme with guarantees superior to random Fourier features in this regime.