A Geometric Approach to Problems in Optimization and Data Science

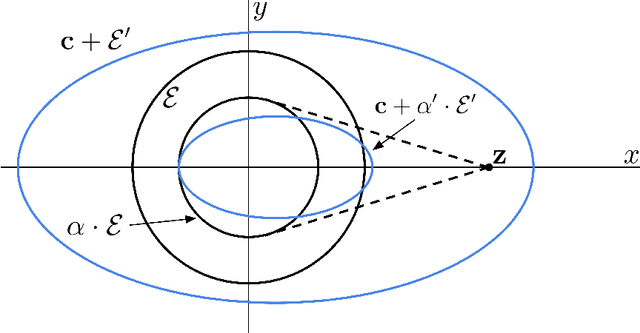
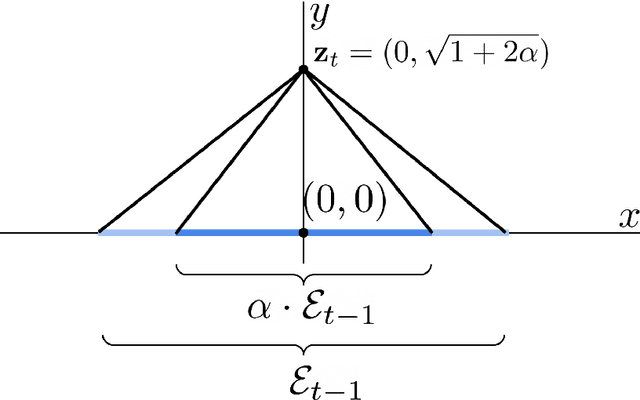
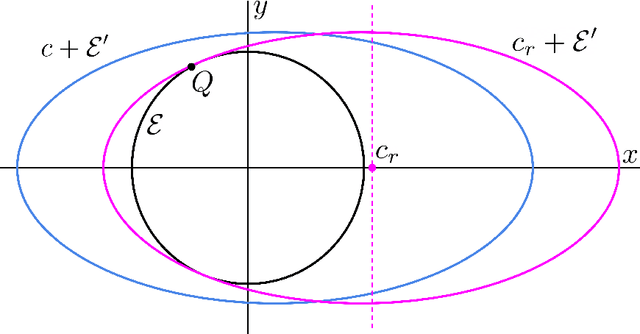
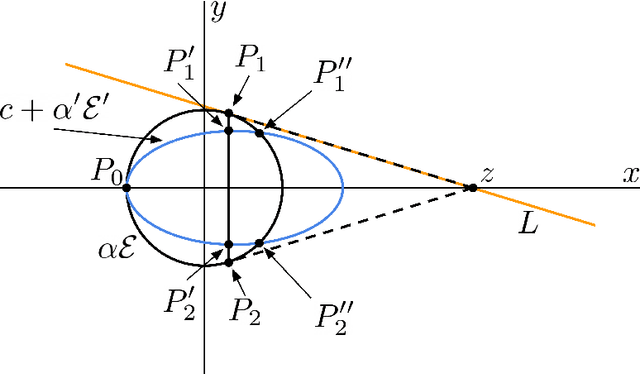
We give new results for problems in computational and statistical machine learning using tools from high-dimensional geometry and probability. We break up our treatment into two parts. In Part I, we focus on computational considerations in optimization. Specifically, we give new algorithms for approximating convex polytopes in a stream, sparsification and robust least squares regression, and dueling optimization. In Part II, we give new statistical guarantees for data science problems. In particular, we formulate a new model in which we analyze statistical properties of backdoor data poisoning attacks, and we study the robustness of graph clustering algorithms to ``helpful'' misspecification.

On the Robustness of Spectral Algorithms for Semirandom Stochastic Block Models

In a graph bisection problem, we are given a graph $G$ with two equally-sized unlabeled communities, and the goal is to recover the vertices in these communities. A popular heuristic, known as spectral clustering, is to output an estimated community assignment based on the eigenvector corresponding to the second smallest eigenvalue of the Laplacian of $G$. Spectral algorithms can be shown to provably recover the cluster structure for graphs generated from certain probabilistic models, such as the Stochastic Block Model (SBM). However, spectral clustering is known to be non-robust to model mis-specification. Techniques based on semidefinite programming have been shown to be more robust, but they incur significant computational overheads. In this work, we study the robustness of spectral algorithms against semirandom adversaries. Informally, a semirandom adversary is allowed to ``helpfully'' change the specification of the model in a way that is consistent with the ground-truth solution. Our semirandom adversaries in particular are allowed to add edges inside clusters or increase the probability that an edge appears inside a cluster. Semirandom adversaries are a useful tool to determine the extent to which an algorithm has overfit to statistical assumptions on the input. On the positive side, we identify classes of semirandom adversaries under which spectral bisection using the _unnormalized_ Laplacian is strongly consistent, i.e., it exactly recovers the planted partitioning. On the negative side, we show that in these classes spectral bisection with the _normalized_ Laplacian outputs a partitioning that makes a classification mistake on a constant fraction of the vertices. Finally, we demonstrate numerical experiments that complement our theoretical findings.

Dueling Optimization with a Monotone Adversary

We introduce and study the problem of dueling optimization with a monotone adversary, which is a generalization of (noiseless) dueling convex optimization. The goal is to design an online algorithm to find a minimizer $\mathbf{x}^{*}$ for a function $f\colon X \to \mathbb{R}$, where $X \subseteq \mathbb{R}^d$. In each round, the algorithm submits a pair of guesses, i.e., $\mathbf{x}^{(1)}$ and $\mathbf{x}^{(2)}$, and the adversary responds with any point in the space that is at least as good as both guesses. The cost of each query is the suboptimality of the worse of the two guesses; i.e., ${\max} \left( f(\mathbf{x}^{(1)}), f(\mathbf{x}^{(2)}) \right) - f(\mathbf{x}^{*})$. The goal is to minimize the number of iterations required to find an $\varepsilon$-optimal point and to minimize the total cost (regret) of the guesses over many rounds. Our main result is an efficient randomized algorithm for several natural choices of the function $f$ and set $X$ that incurs cost $O(d)$ and iteration complexity $O(d\log(1/\varepsilon)^2)$. Moreover, our dependence on $d$ is asymptotically optimal, as we show examples in which any randomized algorithm for this problem must incur $\Omega(d)$ cost and iteration complexity.

Interpolation Learning With Minimum Description Length

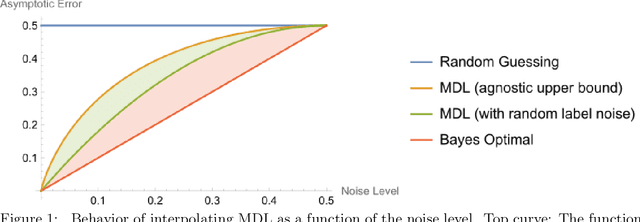
We prove that the Minimum Description Length learning rule exhibits tempered overfitting. We obtain tempered agnostic finite sample learning guarantees and characterize the asymptotic behavior in the presence of random label noise.

Excess Capacity and Backdoor Poisoning

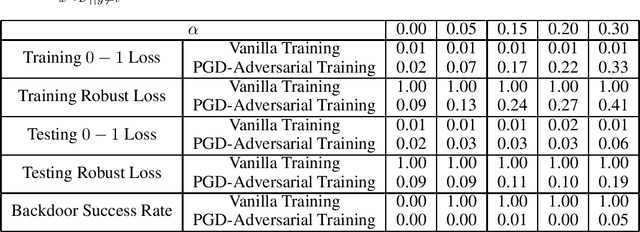
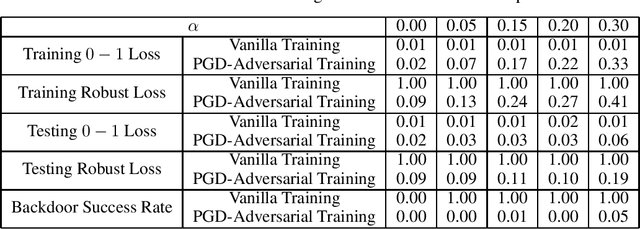
A backdoor data poisoning attack is an adversarial attack wherein the attacker injects several watermarked, mislabeled training examples into a training set. The watermark does not impact the test-time performance of the model on typical data; however, the model reliably errs on watermarked examples. To gain a better foundational understanding of backdoor data poisoning attacks, we present a formal theoretical framework within which one can discuss backdoor data poisoning attacks for classification problems. We then use this to analyze important statistical and computational issues surrounding these attacks. On the statistical front, we identify a parameter we call the memorization capacity that captures the intrinsic vulnerability of a learning problem to a backdoor attack. This allows us to argue about the robustness of several natural learning problems to backdoor attacks. Our results favoring the attacker involve presenting explicit constructions of backdoor attacks, and our robustness results show that some natural problem settings cannot yield successful backdoor attacks. From a computational standpoint, we show that under certain assumptions, adversarial training can detect the presence of backdoors in a training set. We then show that under similar assumptions, two closely related problems we call backdoor filtering and robust generalization are nearly equivalent. This implies that it is both asymptotically necessary and sufficient to design algorithms that can identify watermarked examples in the training set in order to obtain a learning algorithm that both generalizes well to unseen data and is robust to backdoors.