The Role of Environment Access in Agnostic Reinforcement Learning

We study Reinforcement Learning (RL) in environments with large state spaces, where function approximation is required for sample-efficient learning. Departing from a long history of prior work, we consider the weakest possible form of function approximation, called agnostic policy learning, where the learner seeks to find the best policy in a given class $\Pi$, with no guarantee that $\Pi$ contains an optimal policy for the underlying task. Although it is known that sample-efficient agnostic policy learning is not possible in the standard online RL setting without further assumptions, we investigate the extent to which this can be overcome with stronger forms of access to the environment. Specifically, we show that: 1. Agnostic policy learning remains statistically intractable when given access to a local simulator, from which one can reset to any previously seen state. This result holds even when the policy class is realizable, and stands in contrast to a positive result of [MFR24] showing that value-based learning under realizability is tractable with local simulator access. 2. Agnostic policy learning remains statistically intractable when given online access to a reset distribution with good coverage properties over the state space (the so-called $\mu$-reset setting). We also study stronger forms of function approximation for policy learning, showing that PSDP [BKSN03] and CPI [KL02] provably fail in the absence of policy completeness. 3. On a positive note, agnostic policy learning is statistically tractable for Block MDPs with access to both of the above reset models. We establish this via a new algorithm that carefully constructs a policy emulator: a tabular MDP with a small state space that approximates the value functions of all policies $\pi \in \Pi$. These values are approximated without any explicit value function class.

Optimistic Rates for Learning from Label Proportions

We consider a weakly supervised learning problem called Learning from Label Proportions (LLP), where examples are grouped into ``bags'' and only the average label within each bag is revealed to the learner. We study various learning rules for LLP that achieve PAC learning guarantees for classification loss. We establish that the classical Empirical Proportional Risk Minimization (EPRM) learning rule (Yu et al., 2014) achieves fast rates under realizability, but EPRM and similar proportion matching learning rules can fail in the agnostic setting. We also show that (1) a debiased proportional square loss, as well as (2) a recently proposed EasyLLP learning rule (Busa-Fekete et al., 2023) both achieve ``optimistic rates'' (Panchenko, 2002); in both the realizable and agnostic settings, their sample complexity is optimal (up to log factors) in terms of $\epsilon, \delta$, and VC dimension.

Dueling Optimization with a Monotone Adversary

We introduce and study the problem of dueling optimization with a monotone adversary, which is a generalization of (noiseless) dueling convex optimization. The goal is to design an online algorithm to find a minimizer $\mathbf{x}^{*}$ for a function $f\colon X \to \mathbb{R}$, where $X \subseteq \mathbb{R}^d$. In each round, the algorithm submits a pair of guesses, i.e., $\mathbf{x}^{(1)}$ and $\mathbf{x}^{(2)}$, and the adversary responds with any point in the space that is at least as good as both guesses. The cost of each query is the suboptimality of the worse of the two guesses; i.e., ${\max} \left( f(\mathbf{x}^{(1)}), f(\mathbf{x}^{(2)}) \right) - f(\mathbf{x}^{*})$. The goal is to minimize the number of iterations required to find an $\varepsilon$-optimal point and to minimize the total cost (regret) of the guesses over many rounds. Our main result is an efficient randomized algorithm for several natural choices of the function $f$ and set $X$ that incurs cost $O(d)$ and iteration complexity $O(d\log(1/\varepsilon)^2)$. Moreover, our dependence on $d$ is asymptotically optimal, as we show examples in which any randomized algorithm for this problem must incur $\Omega(d)$ cost and iteration complexity.

When is Agnostic Reinforcement Learning Statistically Tractable?

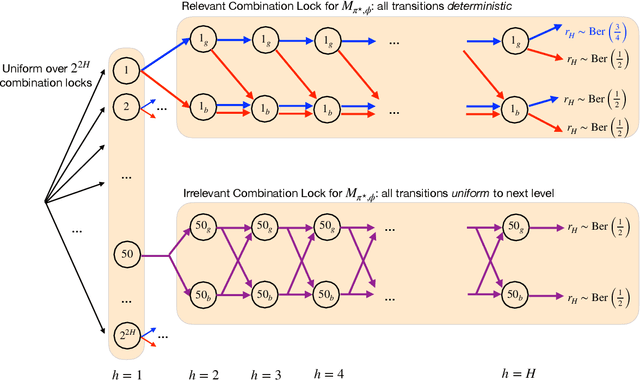
We study the problem of agnostic PAC reinforcement learning (RL): given a policy class $\Pi$, how many rounds of interaction with an unknown MDP (with a potentially large state and action space) are required to learn an $\epsilon$-suboptimal policy with respect to $\Pi$? Towards that end, we introduce a new complexity measure, called the \emph{spanning capacity}, that depends solely on the set $\Pi$ and is independent of the MDP dynamics. With a generative model, we show that for any policy class $\Pi$, bounded spanning capacity characterizes PAC learnability. However, for online RL, the situation is more subtle. We show there exists a policy class $\Pi$ with a bounded spanning capacity that requires a superpolynomial number of samples to learn. This reveals a surprising separation for agnostic learnability between generative access and online access models (as well as between deterministic/stochastic MDPs under online access). On the positive side, we identify an additional \emph{sunflower} structure, which in conjunction with bounded spanning capacity enables statistically efficient online RL via a new algorithm called POPLER, which takes inspiration from classical importance sampling methods as well as techniques for reachable-state identification and policy evaluation in reward-free exploration.

Pessimism for Offline Linear Contextual Bandits using $\ell_p$ Confidence Sets

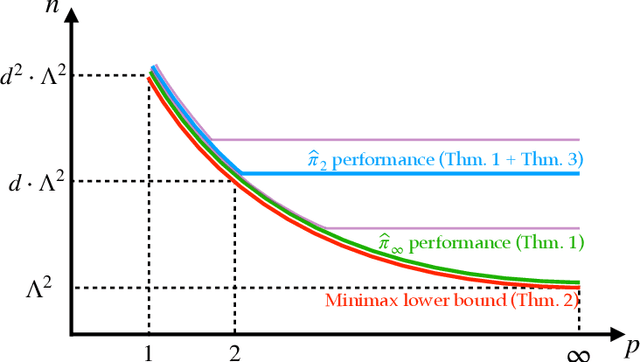
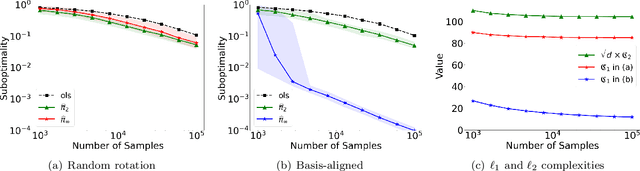
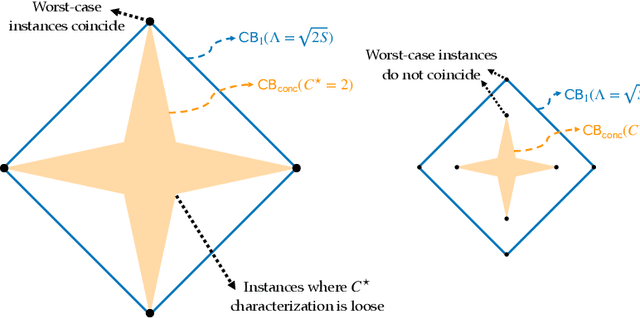
We present a family $\{\hat{\pi}\}_{p\ge 1}$ of pessimistic learning rules for offline learning of linear contextual bandits, relying on confidence sets with respect to different $\ell_p$ norms, where $\hat{\pi}_2$ corresponds to Bellman-consistent pessimism (BCP), while $\hat{\pi}_\infty$ is a novel generalization of lower confidence bound (LCB) to the linear setting. We show that the novel $\hat{\pi}_\infty$ learning rule is, in a sense, adaptively optimal, as it achieves the minimax performance (up to log factors) against all $\ell_q$-constrained problems, and as such it strictly dominates all other predictors in the family, including $\hat{\pi}_2$.

Exponential Family Model-Based Reinforcement Learning via Score Matching

We propose an optimistic model-based algorithm, dubbed SMRL, for finite-horizon episodic reinforcement learning (RL) when the transition model is specified by exponential family distributions with $d$ parameters and the reward is bounded and known. SMRL uses score matching, an unnormalized density estimation technique that enables efficient estimation of the model parameter by ridge regression. Under standard regularity assumptions, SMRL achieves $\tilde O(d\sqrt{H^3T})$ online regret, where $H$ is the length of each episode and $T$ is the total number of interactions (ignoring polynomial dependence on structural scale parameters).

Eluder Dimension and Generalized Rank

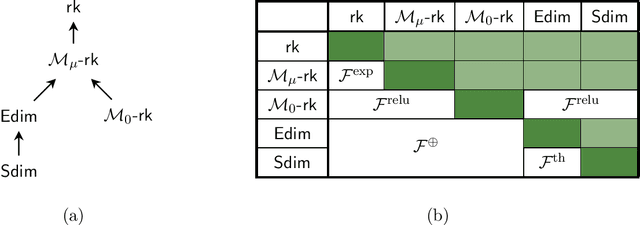
We study the relationship between the eluder dimension for a function class and a generalized notion of rank, defined for any monotone "activation" $\sigma : \mathbb{R} \to \mathbb{R}$, which corresponds to the minimal dimension required to represent the class as a generalized linear model. When $\sigma$ has derivatives bounded away from $0$, it is known that $\sigma$-rank gives rise to an upper bound on eluder dimension for any function class; we show however that eluder dimension can be exponentially smaller than $\sigma$-rank. We also show that the condition on the derivative is necessary; namely, when $\sigma$ is the $\mathrm{relu}$ activation, we show that eluder dimension can be exponentially larger than $\sigma$-rank.