Pessimism for Offline Linear Contextual Bandits using $\ell_p$ Confidence Sets
Paper and Code
May 21, 2022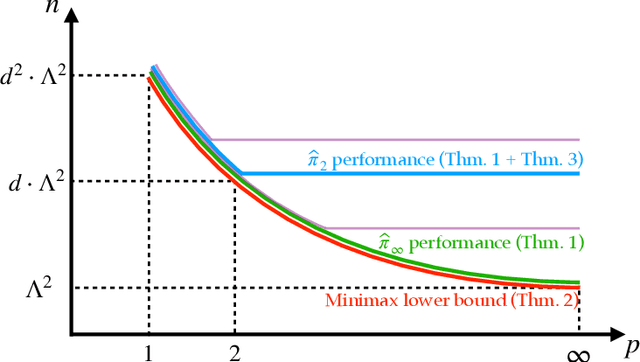
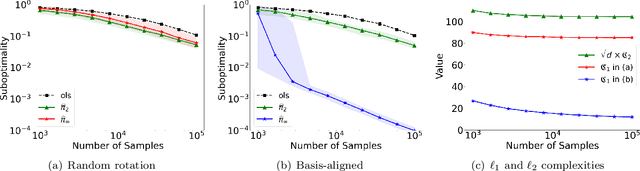
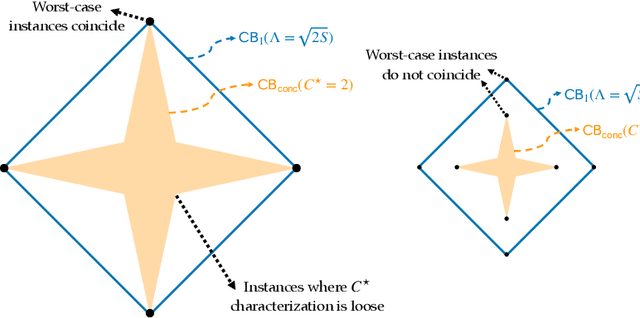
We present a family $\{\hat{\pi}\}_{p\ge 1}$ of pessimistic learning rules for offline learning of linear contextual bandits, relying on confidence sets with respect to different $\ell_p$ norms, where $\hat{\pi}_2$ corresponds to Bellman-consistent pessimism (BCP), while $\hat{\pi}_\infty$ is a novel generalization of lower confidence bound (LCB) to the linear setting. We show that the novel $\hat{\pi}_\infty$ learning rule is, in a sense, adaptively optimal, as it achieves the minimax performance (up to log factors) against all $\ell_q$-constrained problems, and as such it strictly dominates all other predictors in the family, including $\hat{\pi}_2$.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge