Scaling up Kernel Ridge Regression via Locality Sensitive Hashing
Paper and Code
Mar 21, 2020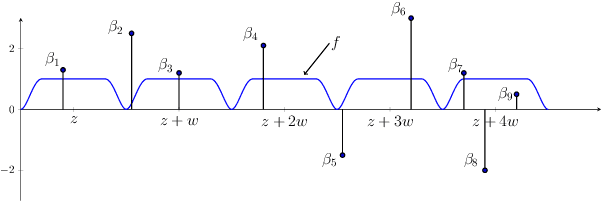
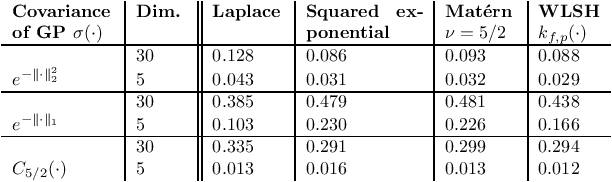
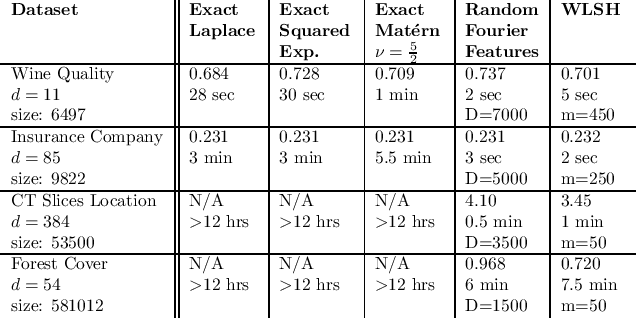
Random binning features, introduced in the seminal paper of Rahimi and Recht (2007), are an efficient method for approximating a kernel matrix using locality sensitive hashing. Random binning features provide a very simple and efficient way of approximating the Laplace kernel but unfortunately do not apply to many important classes of kernels, notably ones that generate smooth Gaussian processes, such as the Gaussian kernel and Matern kernel. In this paper, we introduce a simple weighted version of random binning features and show that the corresponding kernel function generates Gaussian processes of any desired smoothness. We show that our weighted random binning features provide a spectral approximation to the corresponding kernel matrix, leading to efficient algorithms for kernel ridge regression. Experiments on large scale regression datasets show that our method outperforms the accuracy of random Fourier features method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge