Differentially Private Synthetic Data Using KD-Trees

Creation of a synthetic dataset that faithfully represents the data distribution and simultaneously preserves privacy is a major research challenge. Many space partitioning based approaches have emerged in recent years for answering statistical queries in a differentially private manner. However, for synthetic data generation problem, recent research has been mainly focused on deep generative models. In contrast, we exploit space partitioning techniques together with noise perturbation and thus achieve intuitive and transparent algorithms. We propose both data independent and data dependent algorithms for $\epsilon$-differentially private synthetic data generation whose kernel density resembles that of the real dataset. Additionally, we provide theoretical results on the utility-privacy trade-offs and show how our data dependent approach overcomes the curse of dimensionality and leads to a scalable algorithm. We show empirical utility improvements over the prior work, and discuss performance of our algorithm on a downstream classification task on a real dataset.

Efficient and Local Parallel Random Walks

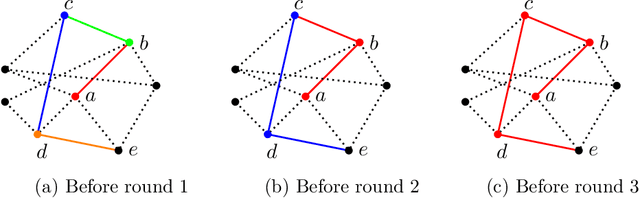
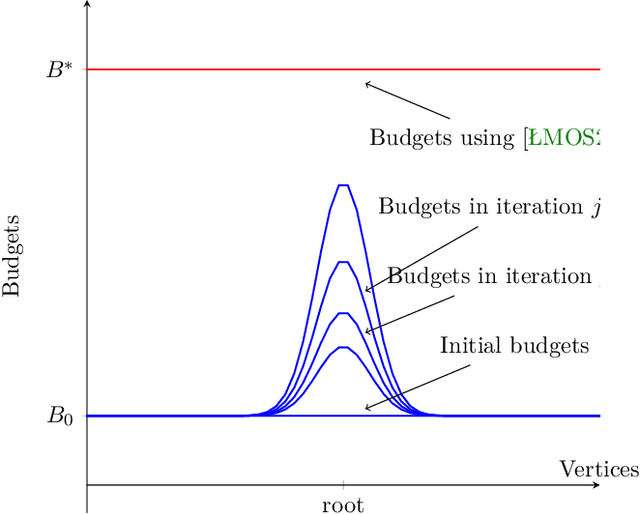
Random walks are a fundamental primitive used in many machine learning algorithms with several applications in clustering and semi-supervised learning. Despite their relevance, the first efficient parallel algorithm to compute random walks has been introduced very recently (Lacki et al.). Unfortunately their method has a fundamental shortcoming: their algorithm is non-local in that it heavily relies on computing random walks out of all nodes in the input graph, even though in many practical applications one is interested in computing random walks only from a small subset of nodes in the graph. In this paper, we present a new algorithm that overcomes this limitation by building random walk efficiently and locally at the same time. We show that our technique is both memory and round efficient, and in particular yields an efficient parallel local clustering algorithm. Finally, we complement our theoretical analysis with experimental results showing that our algorithm is significantly more scalable than previous approaches.

Scaling up Kernel Ridge Regression via Locality Sensitive Hashing

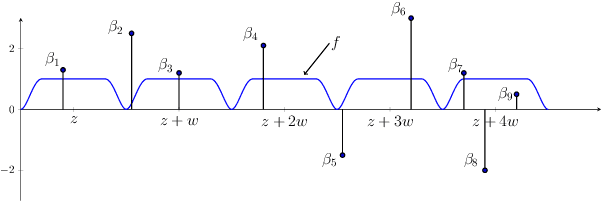
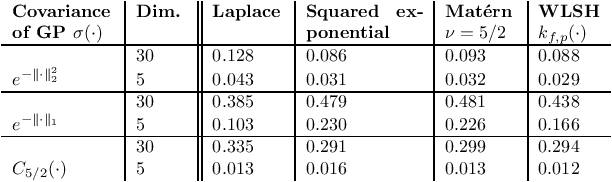
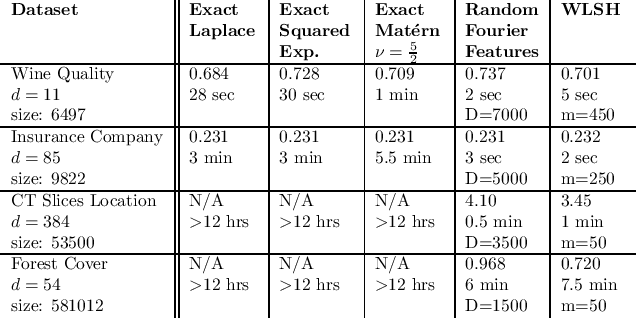
Random binning features, introduced in the seminal paper of Rahimi and Recht (2007), are an efficient method for approximating a kernel matrix using locality sensitive hashing. Random binning features provide a very simple and efficient way of approximating the Laplace kernel but unfortunately do not apply to many important classes of kernels, notably ones that generate smooth Gaussian processes, such as the Gaussian kernel and Matern kernel. In this paper, we introduce a simple weighted version of random binning features and show that the corresponding kernel function generates Gaussian processes of any desired smoothness. We show that our weighted random binning features provide a spectral approximation to the corresponding kernel matrix, leading to efficient algorithms for kernel ridge regression. Experiments on large scale regression datasets show that our method outperforms the accuracy of random Fourier features method.