Even Sparser Graph Transformers

Graph Transformers excel in long-range dependency modeling, but generally require quadratic memory complexity in the number of nodes in an input graph, and hence have trouble scaling to large graphs. Sparse attention variants such as Exphormer can help, but may require high-degree augmentations to the input graph for good performance, and do not attempt to sparsify an already-dense input graph. As the learned attention mechanisms tend to use few of these edges, such high-degree connections may be unnecessary. We show (empirically and with theoretical backing) that attention scores on graphs are usually quite consistent across network widths, and use this observation to propose a two-stage procedure, which we call Spexphormer: first, train a narrow network on the full augmented graph. Next, use only the active connections to train a wider network on a much sparser graph. We establish theoretical conditions when a narrow network's attention scores can match those of a wide network, and show that Spexphormer achieves good performance with drastically reduced memory requirements on various graph datasets.

A Theory for Compressibility of Graph Transformers for Transductive Learning

Transductive tasks on graphs differ fundamentally from typical supervised machine learning tasks, as the independent and identically distributed (i.i.d.) assumption does not hold among samples. Instead, all train/test/validation samples are present during training, making them more akin to a semi-supervised task. These differences make the analysis of the models substantially different from other models. Recently, Graph Transformers have significantly improved results on these datasets by overcoming long-range dependency problems. However, the quadratic complexity of full Transformers has driven the community to explore more efficient variants, such as those with sparser attention patterns. While the attention matrix has been extensively discussed, the hidden dimension or width of the network has received less attention. In this work, we establish some theoretical bounds on how and under what conditions the hidden dimension of these networks can be compressed. Our results apply to both sparse and dense variants of Graph Transformers.

Weisfeiler-Leman at the margin: When more expressivity matters

The Weisfeiler-Leman algorithm ($1$-WL) is a well-studied heuristic for the graph isomorphism problem. Recently, the algorithm has played a prominent role in understanding the expressive power of message-passing graph neural networks (MPNNs) and being effective as a graph kernel. Despite its success, $1$-WL faces challenges in distinguishing non-isomorphic graphs, leading to the development of more expressive MPNN and kernel architectures. However, the relationship between enhanced expressivity and improved generalization performance remains unclear. Here, we show that an architecture's expressivity offers limited insights into its generalization performance when viewed through graph isomorphism. Moreover, we focus on augmenting $1$-WL and MPNNs with subgraph information and employ classical margin theory to investigate the conditions under which an architecture's increased expressivity aligns with improved generalization performance. In addition, we show that gradient flow pushes the MPNN's weights toward the maximum margin solution. Further, we introduce variations of expressive $1$-WL-based kernel and MPNN architectures with provable generalization properties. Our empirical study confirms the validity of our theoretical findings.

Locality-Aware Graph-Rewiring in GNNs

Graph Neural Networks (GNNs) are popular models for machine learning on graphs that typically follow the message-passing paradigm, whereby the feature of a node is updated recursively upon aggregating information over its neighbors. While exchanging messages over the input graph endows GNNs with a strong inductive bias, it can also make GNNs susceptible to over-squashing, thereby preventing them from capturing long-range interactions in the given graph. To rectify this issue, graph rewiring techniques have been proposed as a means of improving information flow by altering the graph connectivity. In this work, we identify three desiderata for graph-rewiring: (i) reduce over-squashing, (ii) respect the locality of the graph, and (iii) preserve the sparsity of the graph. We highlight fundamental trade-offs that occur between spatial and spectral rewiring techniques; while the former often satisfy (i) and (ii) but not (iii), the latter generally satisfy (i) and (iii) at the expense of (ii). We propose a novel rewiring framework that satisfies all of (i)--(iii) through a locality-aware sequence of rewiring operations. We then discuss a specific instance of such rewiring framework and validate its effectiveness on several real-world benchmarks, showing that it either matches or significantly outperforms existing rewiring approaches.

Fast $(1+\varepsilon)$-Approximation Algorithms for Binary Matrix Factorization

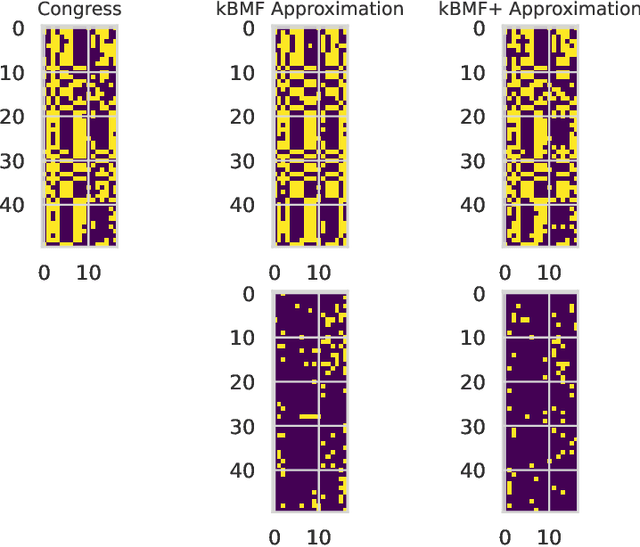
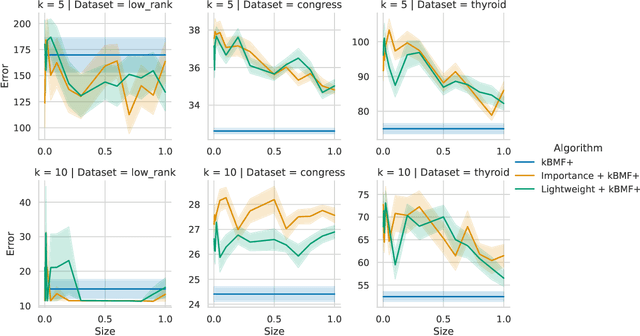
We introduce efficient $(1+\varepsilon)$-approximation algorithms for the binary matrix factorization (BMF) problem, where the inputs are a matrix $\mathbf{A}\in\{0,1\}^{n\times d}$, a rank parameter $k>0$, as well as an accuracy parameter $\varepsilon>0$, and the goal is to approximate $\mathbf{A}$ as a product of low-rank factors $\mathbf{U}\in\{0,1\}^{n\times k}$ and $\mathbf{V}\in\{0,1\}^{k\times d}$. Equivalently, we want to find $\mathbf{U}$ and $\mathbf{V}$ that minimize the Frobenius loss $\|\mathbf{U}\mathbf{V} - \mathbf{A}\|_F^2$. Before this work, the state-of-the-art for this problem was the approximation algorithm of Kumar et. al. [ICML 2019], which achieves a $C$-approximation for some constant $C\ge 576$. We give the first $(1+\varepsilon)$-approximation algorithm using running time singly exponential in $k$, where $k$ is typically a small integer. Our techniques generalize to other common variants of the BMF problem, admitting bicriteria $(1+\varepsilon)$-approximation algorithms for $L_p$ loss functions and the setting where matrix operations are performed in $\mathbb{F}_2$. Our approach can be implemented in standard big data models, such as the streaming or distributed models.

Exphormer: Sparse Transformers for Graphs

Graph transformers have emerged as a promising architecture for a variety of graph learning and representation tasks. Despite their successes, though, it remains challenging to scale graph transformers to large graphs while maintaining accuracy competitive with message-passing networks. In this paper, we introduce Exphormer, a framework for building powerful and scalable graph transformers. Exphormer consists of a sparse attention mechanism based on two mechanisms: virtual global nodes and expander graphs, whose mathematical characteristics, such as spectral expansion, pseduorandomness, and sparsity, yield graph transformers with complexity only linear in the size of the graph, while allowing us to prove desirable theoretical properties of the resulting transformer models. We show that incorporating \textsc{Exphormer} into the recently-proposed GraphGPS framework produces models with competitive empirical results on a wide variety of graph datasets, including state-of-the-art results on three datasets. We also show that \textsc{Exphormer} can scale to datasets on larger graphs than shown in previous graph transformer architectures. Code can be found at https://github.com/hamed1375/Exphormer.

Affinity-Aware Graph Networks

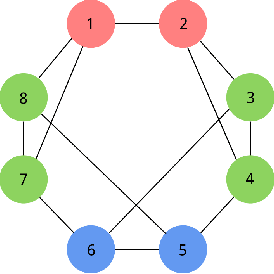
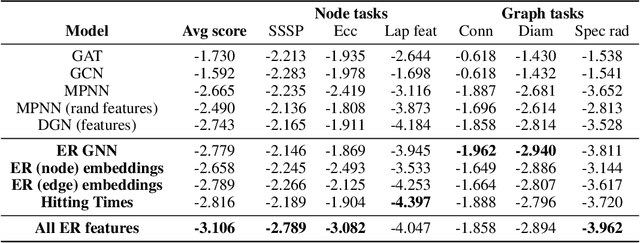
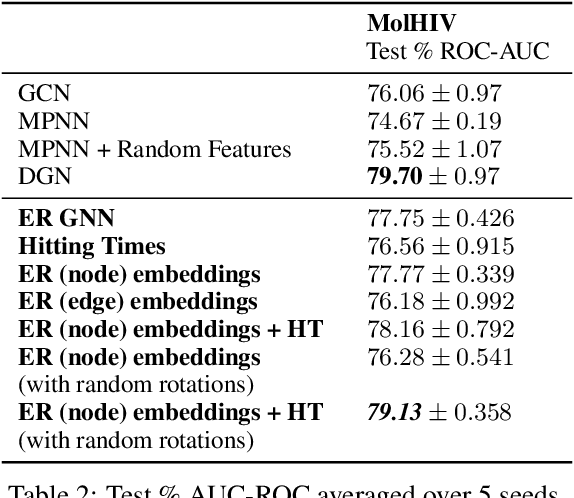
Graph Neural Networks (GNNs) have emerged as a powerful technique for learning on relational data. Owing to the relatively limited number of message passing steps they perform -- and hence a smaller receptive field -- there has been significant interest in improving their expressivity by incorporating structural aspects of the underlying graph. In this paper, we explore the use of affinity measures as features in graph neural networks, in particular measures arising from random walks, including effective resistance, hitting and commute times. We propose message passing networks based on these features and evaluate their performance on a variety of node and graph property prediction tasks. Our architecture has lower computational complexity, while our features are invariant to the permutations of the underlying graph. The measures we compute allow the network to exploit the connectivity properties of the graph, thereby allowing us to outperform relevant benchmarks for a wide variety of tasks, often with significantly fewer message passing steps. On one of the largest publicly available graph regression datasets, OGB-LSC-PCQM4Mv1, we obtain the best known single-model validation MAE at the time of writing.

Private Robust Estimation by Stabilizing Convex Relaxations

We give the first polynomial time and sample $(\epsilon, \delta)$-differentially private (DP) algorithm to estimate the mean, covariance and higher moments in the presence of a constant fraction of adversarial outliers. Our algorithm succeeds for families of distributions that satisfy two well-studied properties in prior works on robust estimation: certifiable subgaussianity of directional moments and certifiable hypercontractivity of degree 2 polynomials. Our recovery guarantees hold in the "right affine-invariant norms": Mahalanobis distance for mean, multiplicative spectral and relative Frobenius distance guarantees for covariance and injective norms for higher moments. Prior works obtained private robust algorithms for mean estimation of subgaussian distributions with bounded covariance. For covariance estimation, ours is the first efficient algorithm (even in the absence of outliers) that succeeds without any condition-number assumptions. Our algorithms arise from a new framework that provides a general blueprint for modifying convex relaxations for robust estimation to satisfy strong worst-case stability guarantees in the appropriate parameter norms whenever the algorithms produce witnesses of correctness in their run. We verify such guarantees for a modification of standard sum-of-squares (SoS) semidefinite programming relaxations for robust estimation. Our privacy guarantees are obtained by combining stability guarantees with a new "estimate dependent" noise injection mechanism in which noise scales with the eigenvalues of the estimated covariance. We believe this framework will be useful more generally in obtaining DP counterparts of robust estimators. Independently of our work, Ashtiani and Liaw [AL21] also obtained a polynomial time and sample private robust estimation algorithm for Gaussian distributions.

Scaling up Kernel Ridge Regression via Locality Sensitive Hashing

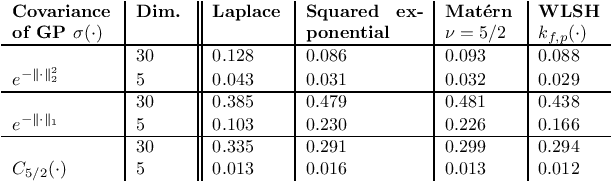
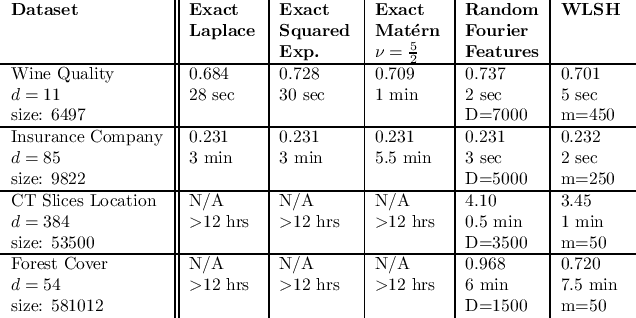
Random binning features, introduced in the seminal paper of Rahimi and Recht (2007), are an efficient method for approximating a kernel matrix using locality sensitive hashing. Random binning features provide a very simple and efficient way of approximating the Laplace kernel but unfortunately do not apply to many important classes of kernels, notably ones that generate smooth Gaussian processes, such as the Gaussian kernel and Matern kernel. In this paper, we introduce a simple weighted version of random binning features and show that the corresponding kernel function generates Gaussian processes of any desired smoothness. We show that our weighted random binning features provide a spectral approximation to the corresponding kernel matrix, leading to efficient algorithms for kernel ridge regression. Experiments on large scale regression datasets show that our method outperforms the accuracy of random Fourier features method.

Private Heavy Hitters and Range Queries in the Shuffled Model

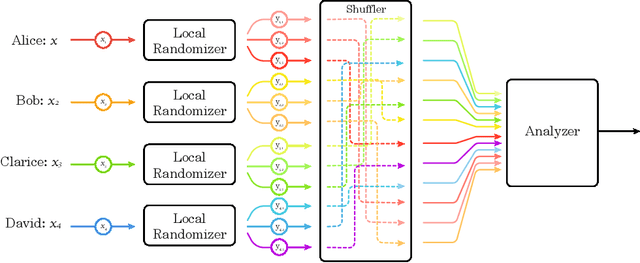
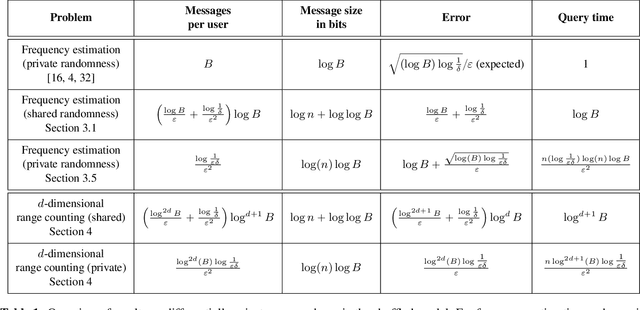
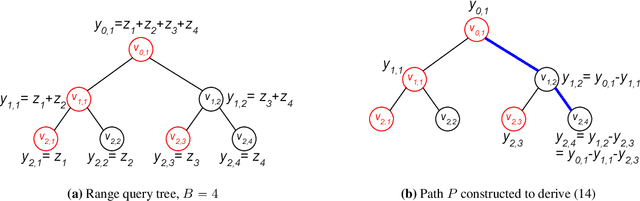
An exciting new development in differential privacy is the shuffled model, which makes it possible to circumvent the large error lower bounds that are typically incurred in the local model, while relying on much weaker trust assumptions than in the central model. In this work, we study two basic statistical problems, namely, heavy hitters and $d$-dimensional range counting queries, in the shuffled model of privacy. For both problems we devise algorithms with polylogarithmic communication per user and polylogarithmic error; a consequence is an algorithm for approximating the median with similar communication and error. These bounds significantly improve on what is possible in the local model of differential privacy, where the error must provably grow polynomially with the number of users.