Even Sparser Graph Transformers

Graph Transformers excel in long-range dependency modeling, but generally require quadratic memory complexity in the number of nodes in an input graph, and hence have trouble scaling to large graphs. Sparse attention variants such as Exphormer can help, but may require high-degree augmentations to the input graph for good performance, and do not attempt to sparsify an already-dense input graph. As the learned attention mechanisms tend to use few of these edges, such high-degree connections may be unnecessary. We show (empirically and with theoretical backing) that attention scores on graphs are usually quite consistent across network widths, and use this observation to propose a two-stage procedure, which we call Spexphormer: first, train a narrow network on the full augmented graph. Next, use only the active connections to train a wider network on a much sparser graph. We establish theoretical conditions when a narrow network's attention scores can match those of a wide network, and show that Spexphormer achieves good performance with drastically reduced memory requirements on various graph datasets.

A Theory for Compressibility of Graph Transformers for Transductive Learning

Transductive tasks on graphs differ fundamentally from typical supervised machine learning tasks, as the independent and identically distributed (i.i.d.) assumption does not hold among samples. Instead, all train/test/validation samples are present during training, making them more akin to a semi-supervised task. These differences make the analysis of the models substantially different from other models. Recently, Graph Transformers have significantly improved results on these datasets by overcoming long-range dependency problems. However, the quadratic complexity of full Transformers has driven the community to explore more efficient variants, such as those with sparser attention patterns. While the attention matrix has been extensively discussed, the hidden dimension or width of the network has received less attention. In this work, we establish some theoretical bounds on how and under what conditions the hidden dimension of these networks can be compressed. Our results apply to both sparse and dense variants of Graph Transformers.

Exphormer: Sparse Transformers for Graphs

Graph transformers have emerged as a promising architecture for a variety of graph learning and representation tasks. Despite their successes, though, it remains challenging to scale graph transformers to large graphs while maintaining accuracy competitive with message-passing networks. In this paper, we introduce Exphormer, a framework for building powerful and scalable graph transformers. Exphormer consists of a sparse attention mechanism based on two mechanisms: virtual global nodes and expander graphs, whose mathematical characteristics, such as spectral expansion, pseduorandomness, and sparsity, yield graph transformers with complexity only linear in the size of the graph, while allowing us to prove desirable theoretical properties of the resulting transformer models. We show that incorporating \textsc{Exphormer} into the recently-proposed GraphGPS framework produces models with competitive empirical results on a wide variety of graph datasets, including state-of-the-art results on three datasets. We also show that \textsc{Exphormer} can scale to datasets on larger graphs than shown in previous graph transformer architectures. Code can be found at https://github.com/hamed1375/Exphormer.

Evaluating Graph Generative Models with Contrastively Learned Features

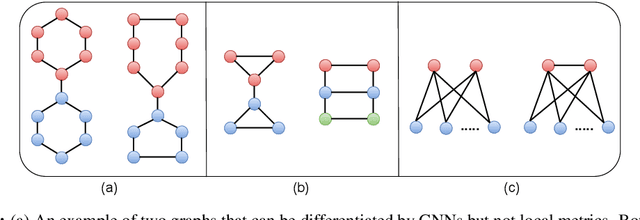
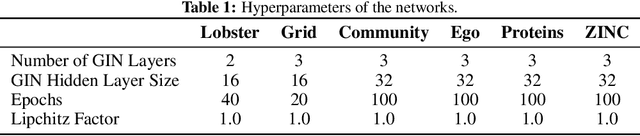
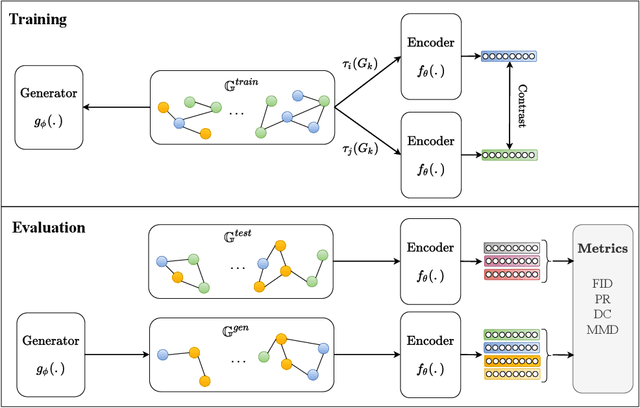
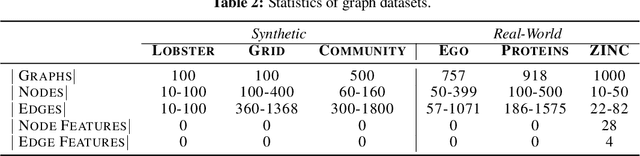
A wide range of models have been proposed for Graph Generative Models, necessitating effective methods to evaluate their quality. So far, most techniques use either traditional metrics based on subgraph counting, or the representations of randomly initialized Graph Neural Networks (GNNs). We propose using representations from contrastively trained GNNs, rather than random GNNs, and show this gives more reliable evaluation metrics. Neither traditional approaches nor GNN-based approaches dominate the other, however: we give examples of graphs that each approach is unable to distinguish. We demonstrate that Graph Substructure Networks (GSNs), which in a way combine both approaches, are better at distinguishing the distances between graph datasets.

TD-GEN: Graph Generation With Tree Decomposition

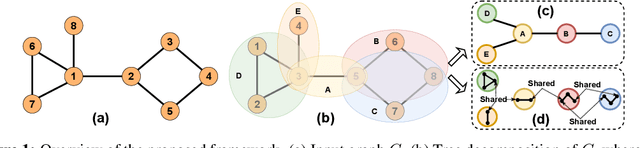
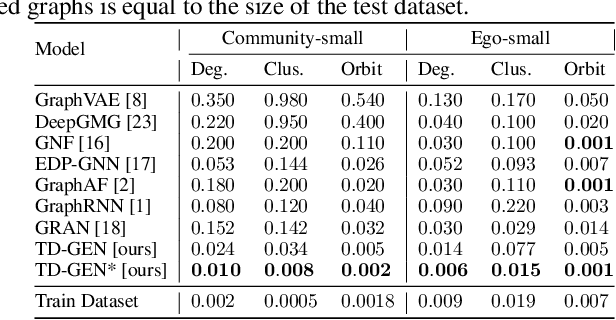
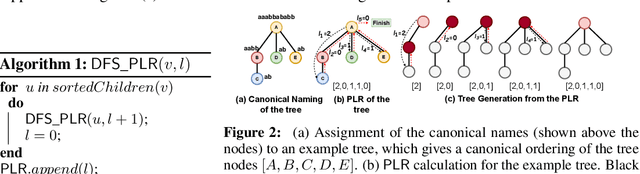
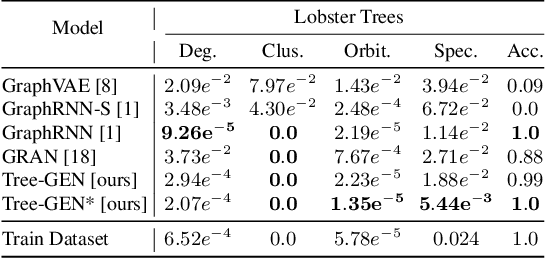
We propose TD-GEN, a graph generation framework based on tree decomposition, and introduce a reduced upper bound on the maximum number of decisions needed for graph generation. The framework includes a permutation invariant tree generation model which forms the backbone of graph generation. Tree nodes are supernodes, each representing a cluster of nodes in the graph. Graph nodes and edges are incrementally generated inside the clusters by traversing the tree supernodes, respecting the structure of the tree decomposition, and following node sharing decisions between the clusters. Finally, we discuss the shortcomings of standard evaluation criteria based on statistical properties of the generated graphs as performance measures. We propose to compare the performance of models based on likelihood. Empirical results on a variety of standard graph generation datasets demonstrate the superior performance of our method.