Optimal Bounds for Private Minimum Spanning Trees via Input Perturbation

We study the problem of privately releasing an approximate minimum spanning tree (MST). Given a graph $G = (V, E, \vec{W})$ where $V$ is a set of $n$ vertices, $E$ is a set of $m$ undirected edges, and $ \vec{W} \in \mathbb{R}^{|E|} $ is an edge-weight vector, our goal is to publish an approximate MST under edge-weight differential privacy, as introduced by Sealfon in PODS 2016, where $V$ and $E$ are considered public and the weight vector is private. Our neighboring relation is $\ell_\infty$-distance on weights: for a sensitivity parameter $\Delta_\infty$, graphs $ G = (V, E, \vec{W}) $ and $ G' = (V, E, \vec{W}') $ are neighboring if $\|\vec{W}-\vec{W}'\|_\infty \leq \Delta_\infty$. Existing private MST algorithms face a trade-off, sacrificing either computational efficiency or accuracy. We show that it is possible to get the best of both worlds: With a suitable random perturbation of the input that does not suffice to make the weight vector private, the result of any non-private MST algorithm will be private and achieves a state-of-the-art error guarantee. Furthermore, by establishing a connection to Private Top-k Selection [Steinke and Ullman, FOCS '17], we give the first privacy-utility trade-off lower bound for MST under approximate differential privacy, demonstrating that the error magnitude, $\tilde{O}(n^{3/2})$, is optimal up to logarithmic factors. That is, our approach matches the time complexity of any non-private MST algorithm and at the same time achieves optimal error. We complement our theoretical treatment with experiments that confirm the practicality of our approach.

Streaming Private Continual Counting via Binning

In differential privacy, $\textit{continual observation}$ refers to problems in which we wish to continuously release a function of a dataset that is revealed one element at a time. The challenge is to maintain a good approximation while keeping the combined output over all time steps differentially private. In the special case of $\textit{continual counting}$ we seek to approximate a sum of binary input elements. This problem has received considerable attention lately, in part due to its relevance in implementations of differentially private stochastic gradient descent. $\textit{Factorization mechanisms}$ are the leading approach to continual counting, but the best such mechanisms do not work well in $\textit{streaming}$ settings since they require space proportional to the size of the input. In this paper, we present a simple approach to approximating factorization mechanisms in low space via $\textit{binning}$, where adjacent matrix entries with similar values are changed to be identical in such a way that a matrix-vector product can be maintained in sublinear space. Our approach has provable sublinear space guarantees for a class of lower triangular matrices whose entries are monotonically decreasing away from the diagonal. We show empirically that even with very low space usage we are able to closely match, and sometimes surpass, the performance of asymptotically optimal factorization mechanisms. Recently, and independently of our work, Dvijotham et al. have also suggested an approach to implementing factorization mechanisms in a streaming setting. Their work differs from ours in several respects: It only addresses factorization into $\textit{Toeplitz}$ matrices, only considers $\textit{maximum}$ error, and uses a different technique based on rational function approximation that seems less versatile than our binning approach.

Faster Private Minimum Spanning Trees

Motivated by applications in clustering and synthetic data generation, we consider the problem of releasing a minimum spanning tree (MST) under edge-weight differential privacy constraints where a graph topology $G=(V,E)$ with $n$ vertices and $m$ edges is public, the weight matrix $\vec{W}\in \mathbb{R}^{n \times n}$ is private, and we wish to release an approximate MST under $\rho$-zero-concentrated differential privacy. Weight matrices are considered neighboring if they differ by at most $\Delta_\infty$ in each entry, i.e., we consider an $\ell_\infty$ neighboring relationship. Existing private MST algorithms either add noise to each entry in $\vec{W}$ and estimate the MST by post-processing or add noise to weights in-place during the execution of a specific MST algorithm. Using the post-processing approach with an efficient MST algorithm takes $O(n^2)$ time on dense graphs but results in an additive error on the weight of the MST of magnitude $O(n^2\log n)$. In-place algorithms give asymptotically better utility, but the running time of existing in-place algorithms is $O(n^3)$ for dense graphs. Our main result is a new differentially private MST algorithm that matches the utility of existing in-place methods while running in time $O(m + n^{3/2}\log n)$ for fixed privacy parameter $\rho$. The technical core of our algorithm is an efficient sublinear time simulation of Report-Noisy-Max that works by discretizing all edge weights to a multiple of $\Delta_\infty$ and forming groups of edges with identical weights. Specifically, we present a data structure that allows us to sample a noisy minimum weight edge among at most $O(n^2)$ cut edges in $O(\sqrt{n} \log n)$ time. Experimental evaluations support our claims that our algorithm significantly improves previous algorithms either in utility or running time.

PLAN: Variance-Aware Private Mean Estimation

Differentially private mean estimation is an important building block in privacy-preserving algorithms for data analysis and machine learning. Though the trade-off between privacy and utility is well understood in the worst case, many datasets exhibit structure that could potentially be exploited to yield better algorithms. In this paper we present $\textit{Private Limit Adapted Noise}$ (PLAN), a family of differentially private algorithms for mean estimation in the setting where inputs are independently sampled from a distribution $\mathcal{D}$ over $\mathbf{R}^d$, with coordinate-wise standard deviations $\boldsymbol{\sigma} \in \mathbf{R}^d$. Similar to mean estimation under Mahalanobis distance, PLAN tailors the shape of the noise to the shape of the data, but unlike previous algorithms the privacy budget is spent non-uniformly over the coordinates. Under a concentration assumption on $\mathcal{D}$, we show how to exploit skew in the vector $\boldsymbol{\sigma}$, obtaining a (zero-concentrated) differentially private mean estimate with $\ell_2$ error proportional to $\|\boldsymbol{\sigma}\|_1$. Previous work has either not taken $\boldsymbol{\sigma}$ into account, or measured error in Mahalanobis distance $\unicode{x2013}$ in both cases resulting in $\ell_2$ error proportional to $\sqrt{d}\|\boldsymbol{\sigma}\|_2$, which can be up to a factor $\sqrt{d}$ larger. To verify the effectiveness of PLAN, we empirically evaluate accuracy on both synthetic and real world data.

A Smooth Binary Mechanism for Efficient Private Continual Observation

In privacy under continual observation we study how to release differentially private estimates based on a dataset that evolves over time. The problem of releasing private prefix sums of $x_1,x_2,x_3,\dots \in\{0,1\}$ (where the value of each $x_i$ is to be private) is particularly well-studied, and a generalized form is used in state-of-the-art methods for private stochastic gradient descent (SGD). The seminal binary mechanism privately releases the first $t$ prefix sums with noise of variance polylogarithmic in $t$. Recently, Henzinger et al. and Denisov et al. showed that it is possible to improve on the binary mechanism in two ways: The variance of the noise can be reduced by a (large) constant factor, and also made more even across time steps. However, their algorithms for generating the noise distribution are not as efficient as one would like in terms of computation time and (in particular) space. We address the efficiency problem by presenting a simple alternative to the binary mechanism in which 1) generating the noise takes constant average time per value, 2) the variance is reduced by a factor about 4 compared to the binary mechanism, and 3) the noise distribution at each step is identical. Empirically, a simple Python implementation of our approach outperforms the running time of the approach of Henzinger et al., as well as an attempt to improve their algorithm using high-performance algorithms for multiplication with Toeplitz matrices.

Daisy Bloom Filters

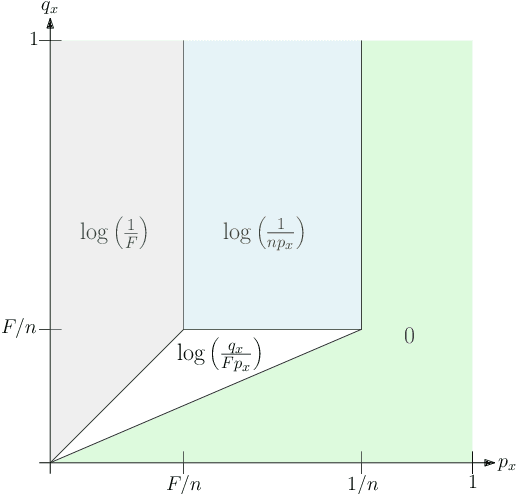
Weighted Bloom filters (Bruck, Gao and Jiang, ISIT 2006) are Bloom filters that adapt the number of hash functions according to the query element. That is, they use a sequence of hash functions $h_1, h_2, \dots$ and insert $x$ by setting the bits in $k_x$ positions $h_1(x), h_2(x), \dots, h_{k_x}(x)$ to 1, where the parameter $k_x$ depends on $x$. Similarly, a query for $x$ checks whether the bits at positions $h_1(x), h_2(x), \dots, h_{k_x}(x)$ contain a $0$ (in which case we know that $x$ was not inserted), or contains only $1$s (in which case $x$ may have been inserted, but it could also be a false positive). In this paper, we determine a near-optimal choice of the parameters $k_x$ in a model where $n$ elements are inserted independently from a probability distribution $\mathcal{P}$ and query elements are chosen from a probability distribution $\mathcal{Q}$, under a bound on the false positive probability $F$. In contrast, the parameter choice of Bruck et al., as well as follow-up work by Wang et al., does not guarantee a nontrivial bound on the false positive rate. We refer to our parameterization of the weighted Bloom filter as a $\textit{Daisy Bloom filter}$. For many distributions $\mathcal{P}$ and $\mathcal{Q}$, the Daisy Bloom filter space usage is significantly smaller than that of Standard Bloom filters. Our upper bound is complemented with an information-theoretical lower bound, showing that (with mild restrictions on the distributions $\mathcal{P}$ and $\mathcal{Q}$), the space usage of Daisy Bloom filters is the best possible up to a constant factor. Daisy Bloom filters can be seen as a fine-grained variant of a recent data structure of Vaidya, Knorr, Mitzenmacher and Kraska. Like their work, we are motivated by settings in which we have prior knowledge of the workload of the filter, possibly in the form of advice from a machine learning algorithm.

Infinitely Divisible Noise in the Low Privacy Regime

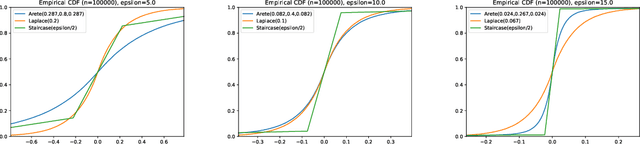
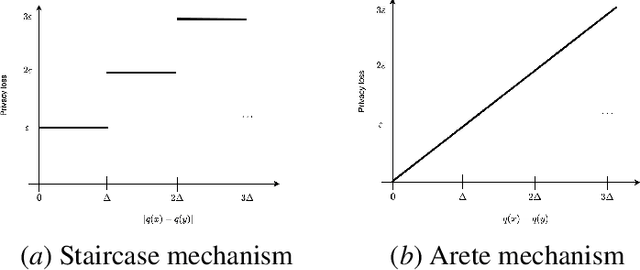
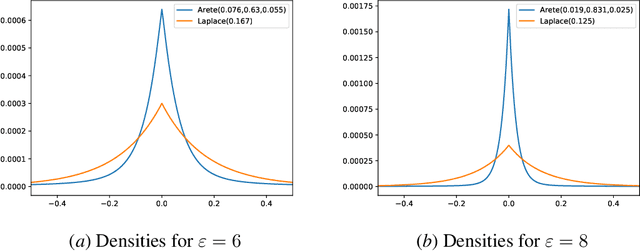
Federated learning, in which training data is distributed among users and never shared, has emerged as a popular approach to privacy-preserving machine learning. Cryptographic techniques such as secure aggregation are used to aggregate contributions, like a model update, from all users. A robust technique for making such aggregates differentially private is to exploit infinite divisibility of the Laplace distribution, namely, that a Laplace distribution can be expressed as a sum of i.i.d. noise shares from a Gamma distribution, one share added by each user. However, Laplace noise is known to have suboptimal error in the low privacy regime for $\varepsilon$-differential privacy, where $\varepsilon > 1$ is a large constant. In this paper we present the first infinitely divisible noise distribution for real-valued data that achieves $\varepsilon$-differential privacy and has expected error that decreases exponentially with $\varepsilon$.

DEANN: Speeding up Kernel-Density Estimation using Approximate Nearest Neighbor Search

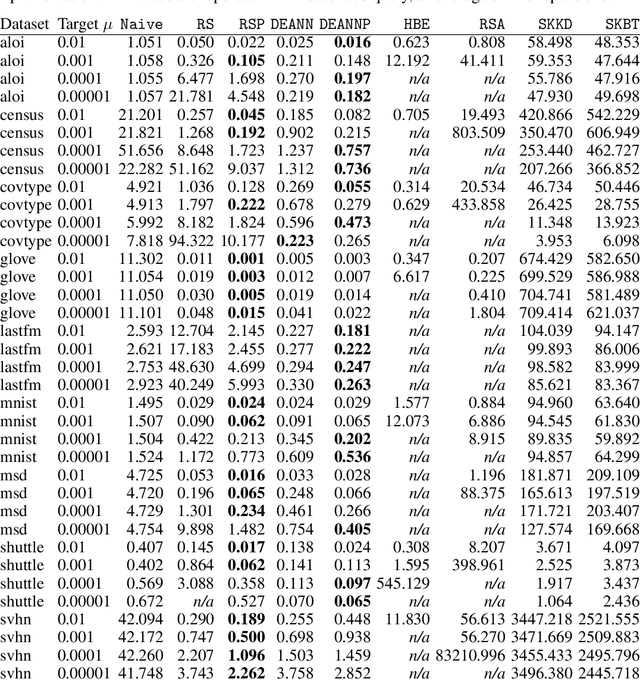
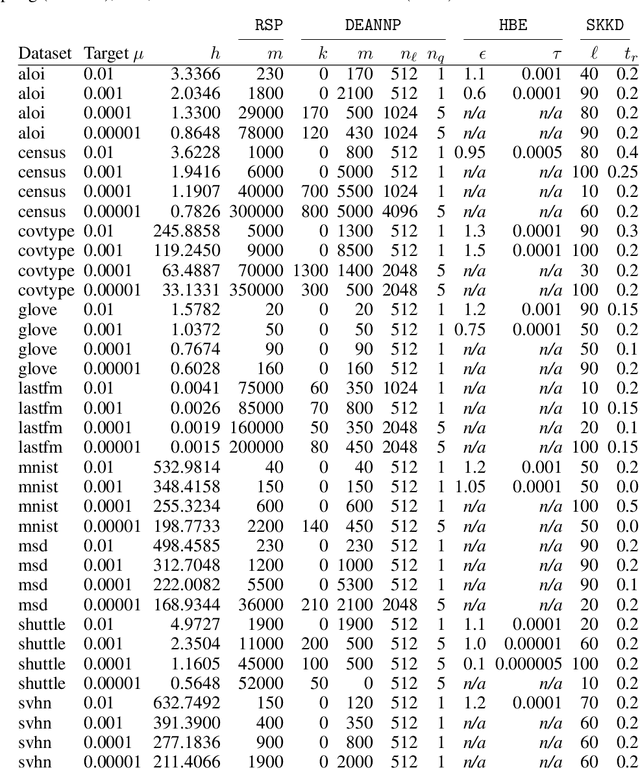
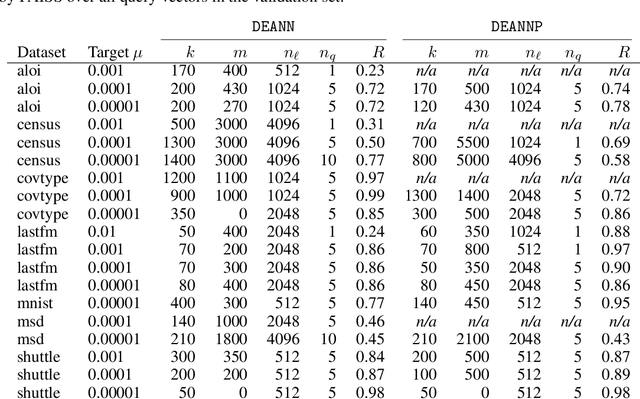
Kernel Density Estimation (KDE) is a nonparametric method for estimating the shape of a density function, given a set of samples from the distribution. Recently, locality-sensitive hashing, originally proposed as a tool for nearest neighbor search, has been shown to enable fast KDE data structures. However, these approaches do not take advantage of the many other advances that have been made in algorithms for nearest neighbor algorithms. We present an algorithm called Density Estimation from Approximate Nearest Neighbors (DEANN) where we apply Approximate Nearest Neighbor (ANN) algorithms as a black box subroutine to compute an unbiased KDE. The idea is to find points that have a large contribution to the KDE using ANN, compute their contribution exactly, and approximate the remainder with Random Sampling (RS). We present a theoretical argument that supports the idea that an ANN subroutine can speed up the evaluation. Furthermore, we provide a C++ implementation with a Python interface that can make use of an arbitrary ANN implementation as a subroutine for KDE evaluation. We show empirically that our implementation outperforms state of the art implementations in all high dimensional datasets we considered, and matches the performance of RS in cases where the ANN yield no gains in performance.

CountSketches, Feature Hashing and the Median of Three

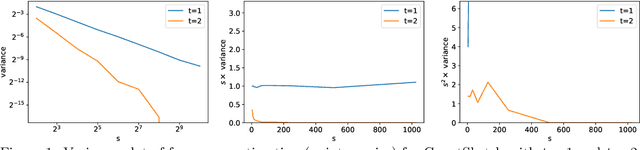
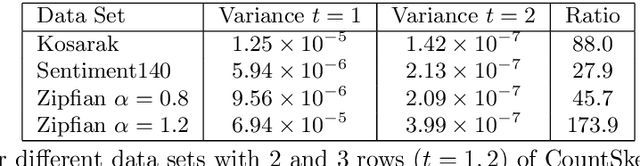
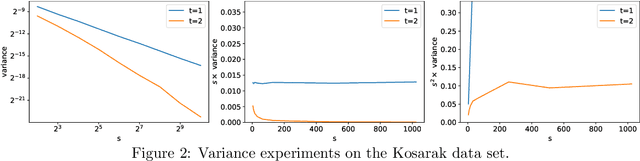
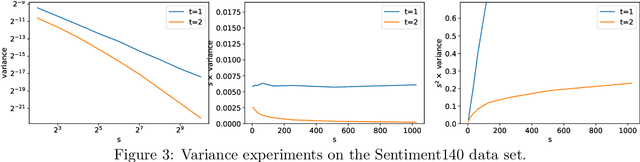
In this paper, we revisit the classic CountSketch method, which is a sparse, random projection that transforms a (high-dimensional) Euclidean vector $v$ to a vector of dimension $(2t-1) s$, where $t, s > 0$ are integer parameters. It is known that even for $t=1$, a CountSketch allows estimating coordinates of $v$ with variance bounded by $\|v\|_2^2/s$. For $t > 1$, the estimator takes the median of $2t-1$ independent estimates, and the probability that the estimate is off by more than $2 \|v\|_2/\sqrt{s}$ is exponentially small in $t$. This suggests choosing $t$ to be logarithmic in a desired inverse failure probability. However, implementations of CountSketch often use a small, constant $t$. Previous work only predicts a constant factor improvement in this setting. Our main contribution is a new analysis of Count-Sketch, showing an improvement in variance to $O(\min\{\|v\|_1^2/s^2,\|v\|_2^2/s\})$ when $t > 1$. That is, the variance decreases proportionally to $s^{-2}$, asymptotically for large enough $s$. We also study the variance in the setting where an inner product is to be estimated from two CountSketches. This finding suggests that the Feature Hashing method, which is essentially identical to CountSketch but does not make use of the median estimator, can be made more reliable at a small cost in settings where using a median estimator is possible. We confirm our theoretical findings in experiments and thereby help justify why a small constant number of estimates often suffice in practice. Our improved variance bounds are based on new general theorems about the variance and higher moments of the median of i.i.d. random variables that may be of independent interest.

Sampling a Near Neighbor in High Dimensions -- Who is the Fairest of Them All?

Similarity search is a fundamental algorithmic primitive, widely used in many computer science disciplines. Given a set of points $S$ and a radius parameter $r>0$, the $r$-near neighbor ($r$-NN) problem asks for a data structure that, given any query point $q$, returns a point $p$ within distance at most $r$ from $q$. In this paper, we study the $r$-NN problem in the light of individual fairness and providing equal opportunities: all points that are within distance $r$ from the query should have the same probability to be returned. In the low-dimensional case, this problem was first studied by Hu, Qiao, and Tao (PODS 2014). Locality sensitive hashing (LSH), the theoretically strongest approach to similarity search in high dimensions, does not provide such a fairness guarantee. In this work, we show that LSH based algorithms can be made fair, without a significant loss in efficiency. We propose several efficient data structures for the exact and approximate variants of the fair NN problem. Our approach works more generally for sampling uniformly from a sub-collection of sets of a given collection and can be used in a few other applications. We also develop a data structure for fair similarity search under inner product that requires nearly-linear space and exploits locality sensitive filters. The paper concludes with an experimental evaluation that highlights the inherent unfairness of NN data structures and shows the performance of our algorithms on real-world datasets.