Infinitely Divisible Noise in the Low Privacy Regime
Paper and Code
Oct 18, 2021
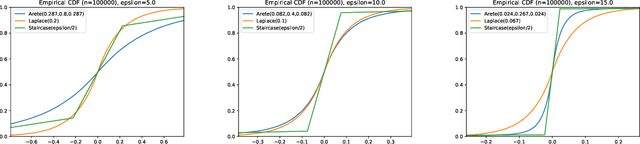
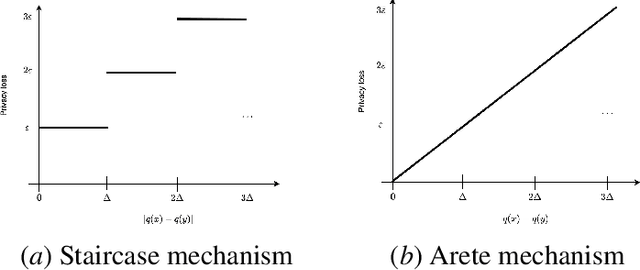
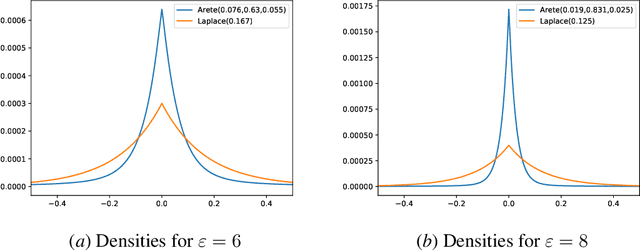
Federated learning, in which training data is distributed among users and never shared, has emerged as a popular approach to privacy-preserving machine learning. Cryptographic techniques such as secure aggregation are used to aggregate contributions, like a model update, from all users. A robust technique for making such aggregates differentially private is to exploit infinite divisibility of the Laplace distribution, namely, that a Laplace distribution can be expressed as a sum of i.i.d. noise shares from a Gamma distribution, one share added by each user. However, Laplace noise is known to have suboptimal error in the low privacy regime for $\varepsilon$-differential privacy, where $\varepsilon > 1$ is a large constant. In this paper we present the first infinitely divisible noise distribution for real-valued data that achieves $\varepsilon$-differential privacy and has expected error that decreases exponentially with $\varepsilon$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge