Ioana O. Bercea
Daisy Bloom Filters
May 30, 2022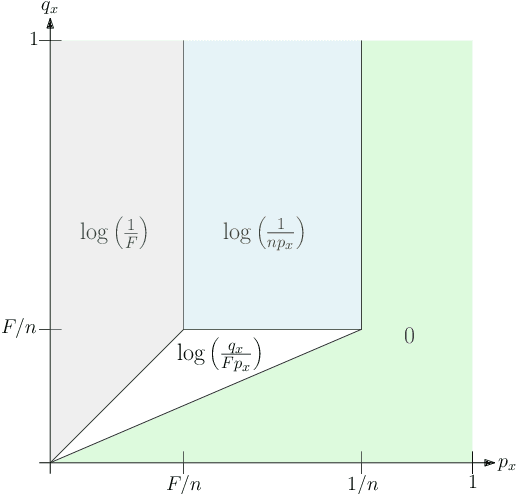
Abstract:Weighted Bloom filters (Bruck, Gao and Jiang, ISIT 2006) are Bloom filters that adapt the number of hash functions according to the query element. That is, they use a sequence of hash functions $h_1, h_2, \dots$ and insert $x$ by setting the bits in $k_x$ positions $h_1(x), h_2(x), \dots, h_{k_x}(x)$ to 1, where the parameter $k_x$ depends on $x$. Similarly, a query for $x$ checks whether the bits at positions $h_1(x), h_2(x), \dots, h_{k_x}(x)$ contain a $0$ (in which case we know that $x$ was not inserted), or contains only $1$s (in which case $x$ may have been inserted, but it could also be a false positive). In this paper, we determine a near-optimal choice of the parameters $k_x$ in a model where $n$ elements are inserted independently from a probability distribution $\mathcal{P}$ and query elements are chosen from a probability distribution $\mathcal{Q}$, under a bound on the false positive probability $F$. In contrast, the parameter choice of Bruck et al., as well as follow-up work by Wang et al., does not guarantee a nontrivial bound on the false positive rate. We refer to our parameterization of the weighted Bloom filter as a $\textit{Daisy Bloom filter}$. For many distributions $\mathcal{P}$ and $\mathcal{Q}$, the Daisy Bloom filter space usage is significantly smaller than that of Standard Bloom filters. Our upper bound is complemented with an information-theoretical lower bound, showing that (with mild restrictions on the distributions $\mathcal{P}$ and $\mathcal{Q}$), the space usage of Daisy Bloom filters is the best possible up to a constant factor. Daisy Bloom filters can be seen as a fine-grained variant of a recent data structure of Vaidya, Knorr, Mitzenmacher and Kraska. Like their work, we are motivated by settings in which we have prior knowledge of the workload of the filter, possibly in the form of advice from a machine learning algorithm.
Minimizing Uncertainty through Sensor Placement with Angle Constraints
Jul 20, 2016
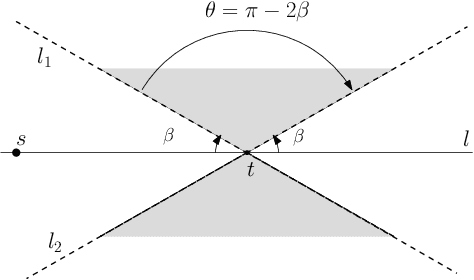
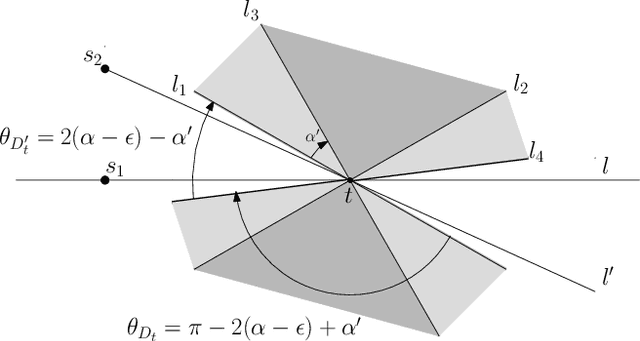
Abstract:We study the problem of sensor placement in environments in which localization is a necessity, such as ad-hoc wireless sensor networks that allow the placement of a few anchors that know their location or sensor arrays that are tracking a target. In most of these situations, the quality of localization depends on the relative angle between the target and the pair of sensors observing it. In this paper, we consider placing a small number of sensors which ensure good angular $\alpha$-coverage: given $\alpha$ in $[0,\pi/2]$, for each target location $t$, there must be at least two sensors $s_1$ and $s_2$ such that the $\angle(s_1 t s_2)$ is in the interval $[\alpha, \pi-\alpha]$. One of the main difficulties encountered in such problems is that since the constraints depend on at least two sensors, building a solution must account for the inherent dependency between selected sensors, a feature that generic Set Cover techniques do not account for. We introduce a general framework that guarantees an angular coverage that is arbitrarily close to $\alpha$ for any $\alpha <= \pi/3$ and apply it to a variety of problems to get bi-criteria approximations. When the angular coverage is required to be at least a constant fraction of $\alpha$, we obtain results that are strictly better than what standard geometric Set Cover methods give. When the angular coverage is required to be at least $(1-1/\delta)\cdot\alpha$, we obtain a $\mathcal{O}(\log \delta)$- approximation for sensor placement with $\alpha$-coverage on the plane. In the presence of additional distance or visibility constraints, the framework gives a $\mathcal{O}(\log\delta\cdot\log k_{OPT})$-approximation, where $k_{OPT}$ is the size of the optimal solution. We also use our framework to give a $\mathcal{O}(\log \delta)$-approximation that ensures $(1-1/\delta)\cdot \alpha$-coverage and covers every target within distance $3R$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge