Minimizing Uncertainty through Sensor Placement with Angle Constraints
Paper and Code
Jul 20, 2016
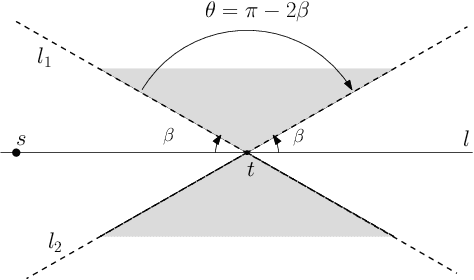
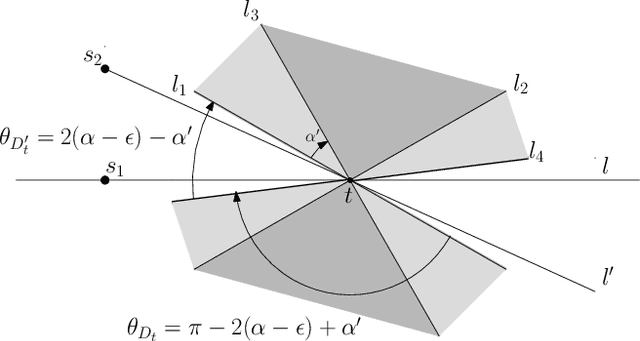
We study the problem of sensor placement in environments in which localization is a necessity, such as ad-hoc wireless sensor networks that allow the placement of a few anchors that know their location or sensor arrays that are tracking a target. In most of these situations, the quality of localization depends on the relative angle between the target and the pair of sensors observing it. In this paper, we consider placing a small number of sensors which ensure good angular $\alpha$-coverage: given $\alpha$ in $[0,\pi/2]$, for each target location $t$, there must be at least two sensors $s_1$ and $s_2$ such that the $\angle(s_1 t s_2)$ is in the interval $[\alpha, \pi-\alpha]$. One of the main difficulties encountered in such problems is that since the constraints depend on at least two sensors, building a solution must account for the inherent dependency between selected sensors, a feature that generic Set Cover techniques do not account for. We introduce a general framework that guarantees an angular coverage that is arbitrarily close to $\alpha$ for any $\alpha <= \pi/3$ and apply it to a variety of problems to get bi-criteria approximations. When the angular coverage is required to be at least a constant fraction of $\alpha$, we obtain results that are strictly better than what standard geometric Set Cover methods give. When the angular coverage is required to be at least $(1-1/\delta)\cdot\alpha$, we obtain a $\mathcal{O}(\log \delta)$- approximation for sensor placement with $\alpha$-coverage on the plane. In the presence of additional distance or visibility constraints, the framework gives a $\mathcal{O}(\log\delta\cdot\log k_{OPT})$-approximation, where $k_{OPT}$ is the size of the optimal solution. We also use our framework to give a $\mathcal{O}(\log \delta)$-approximation that ensures $(1-1/\delta)\cdot \alpha$-coverage and covers every target within distance $3R$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge